Math

  • Fraction: A portion of a complete entity, expressed as a ratio.
  • Percentage: A value expressed as a part of 100.

a/b:

a = numerator (top part of the fraction)
b = denominator (bottom part of the fraction, represented by “d” for down)

Order of Operations

PEMDAS (Order of Operations)

  • P: Parentheses
  • E: Exponents (or roots)
    • M: Multiplication
    • D: Division
      • Perform multiplication and division in the order they occur from left to right.
    • A: Addition
    • S: Subtraction
      • Perform addition and subtraction in the order they appear from left to right.

Example:
2 + 5 × 8

  1. Perform multiplication first.
  2. Then, proceed with addition.

Example:
(4 – 6) × ÷ 8

  1. Begin with parentheses.
  2. Then, calculate the root (if applicable).
  3. Follow with multiplication or division.
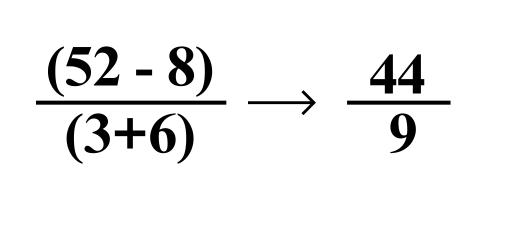
Fractions: Complete all operations in the numerator and denominator before performing the division.

Standard & Metric Conversions

1 gal ………………………………… 3.8L

1 kg ………………………………… 2.2 lb

1 in ………………………………… 2.54 cm

1 m ………………………………… 3.28 ft

1 mi ………………………………… 1.6 km

1 oz ………………………………… 28.35 g

1 m ………………………………… 1.09 yd

Prefixes

kilo ………………………………… 1,000

deca …………………………………… 10

deci ………………………………… 1/10

centi ……………………………… 1/100

milli …………………………….. 1/1000

micro ……………………… 1,000,000

Value of Variable

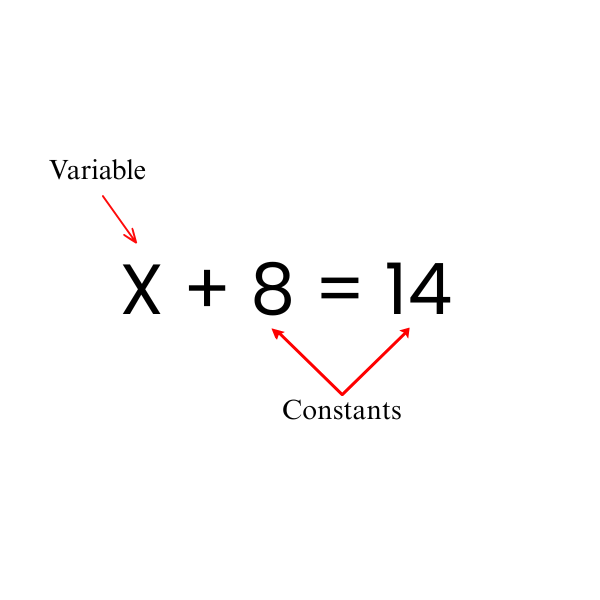
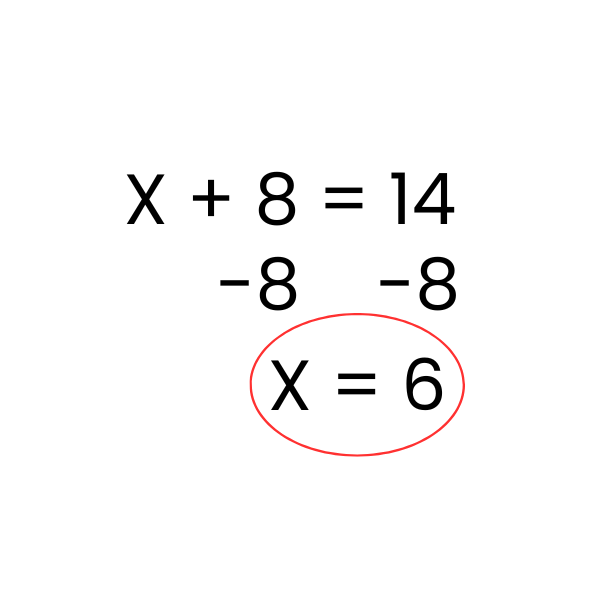
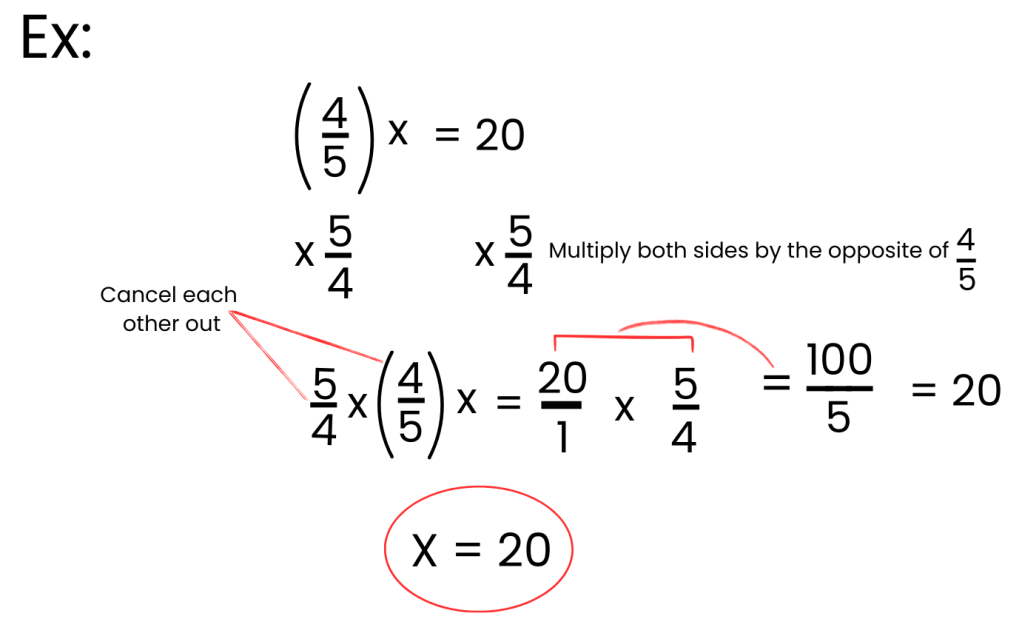
Isolate constants on one side of the equals sign and variables on the other by applying inverse operations.
Separate the variable, then determine its value.

Rounding

Round up when the digit in the smallest place is 5 or higher.
Round to the nearest tenth:
Approximate to the closest thousandths place:
Round to the closest whole number:

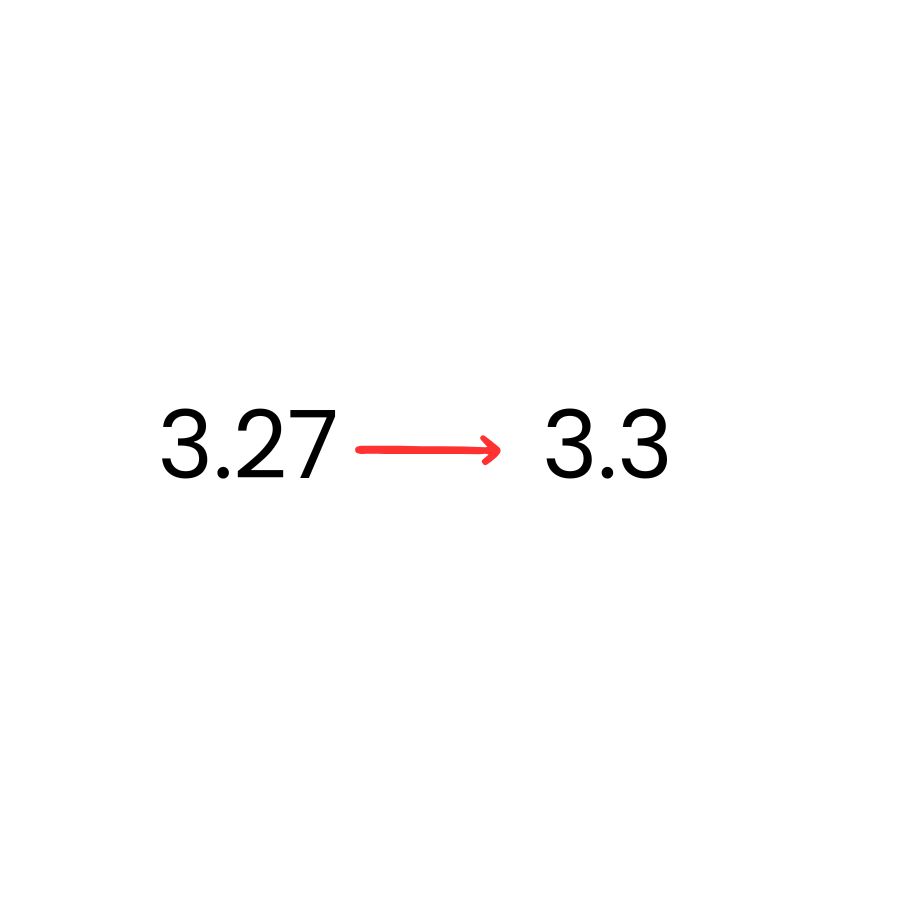
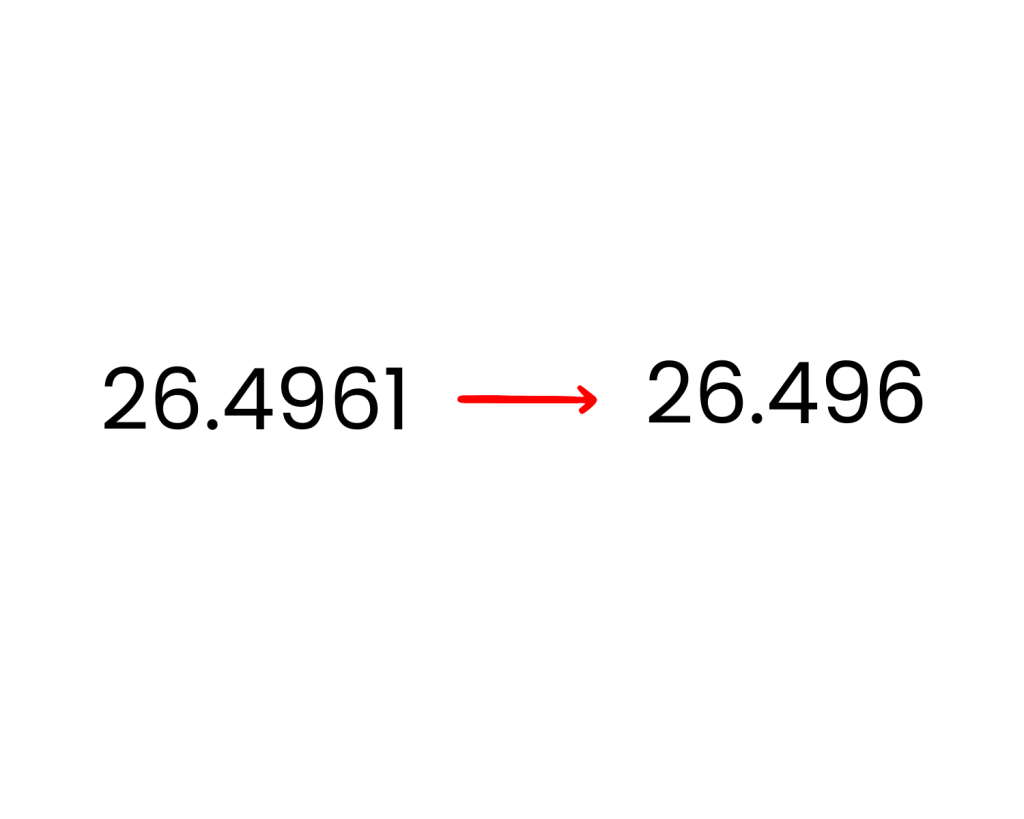
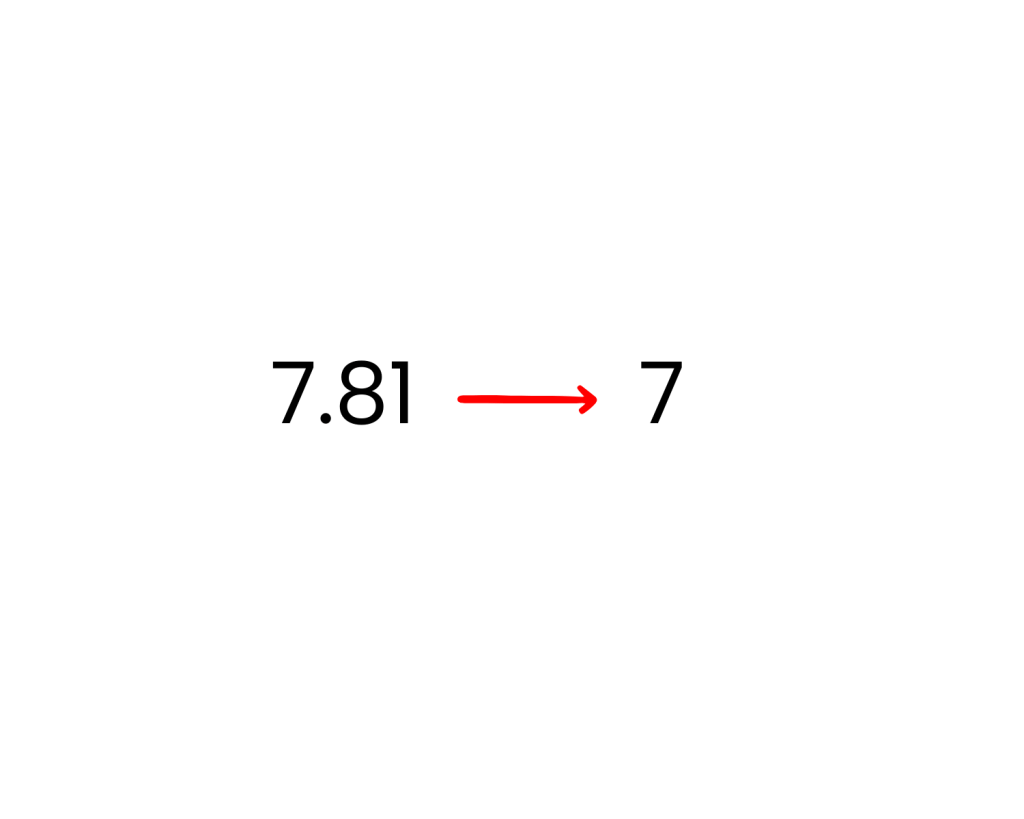
Rate of Change

Ratio: the frequency one number fits into another.

Ex: 7/1

Rate: a comparative ratio expressed with specific units.

Ex: 7miles/Hour

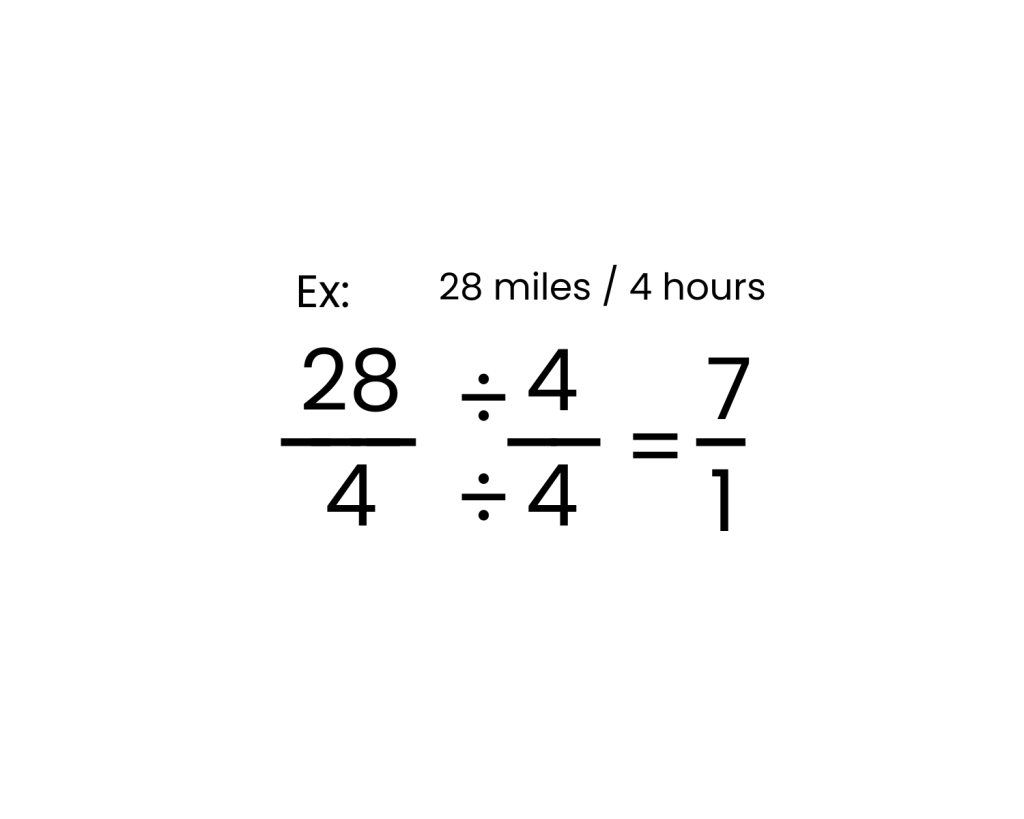
If the denominator is not 1: divide the numerator and denominator by the denominator to determine the rate.

Determining the slope of a line using two points:

  1. Select any two plotted points.
  2. Divide the difference in y-coordinates by the difference in x-coordinates.

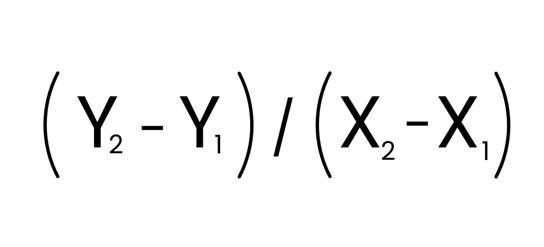
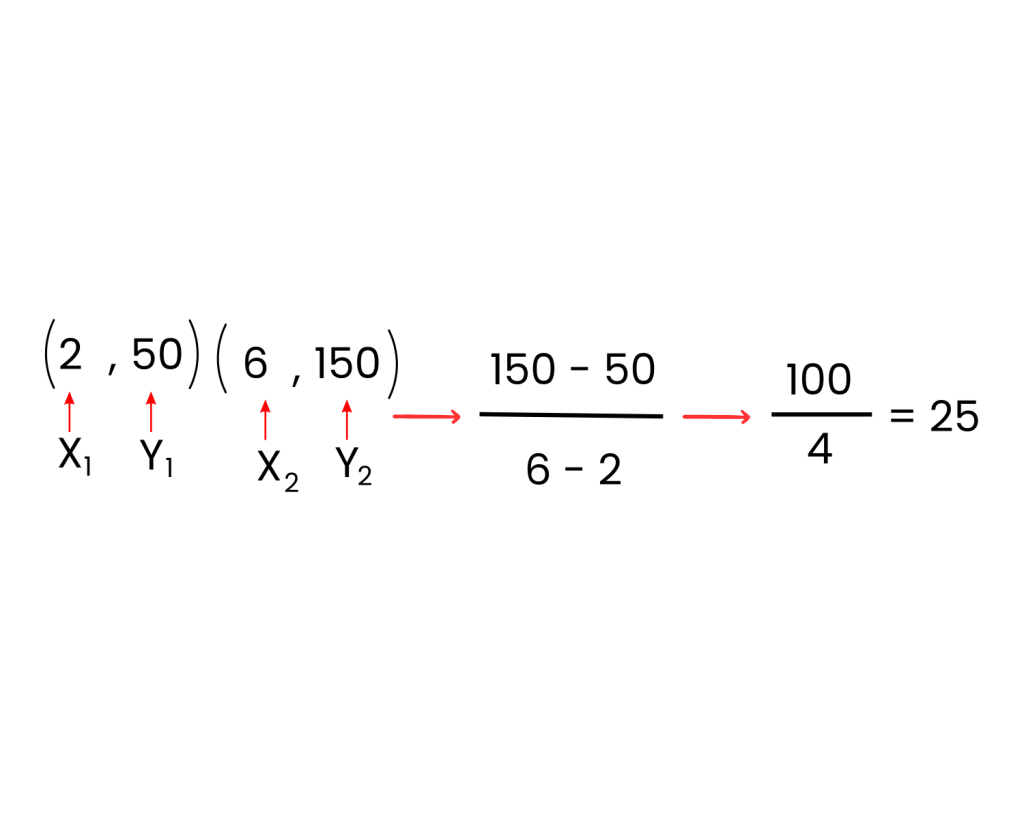
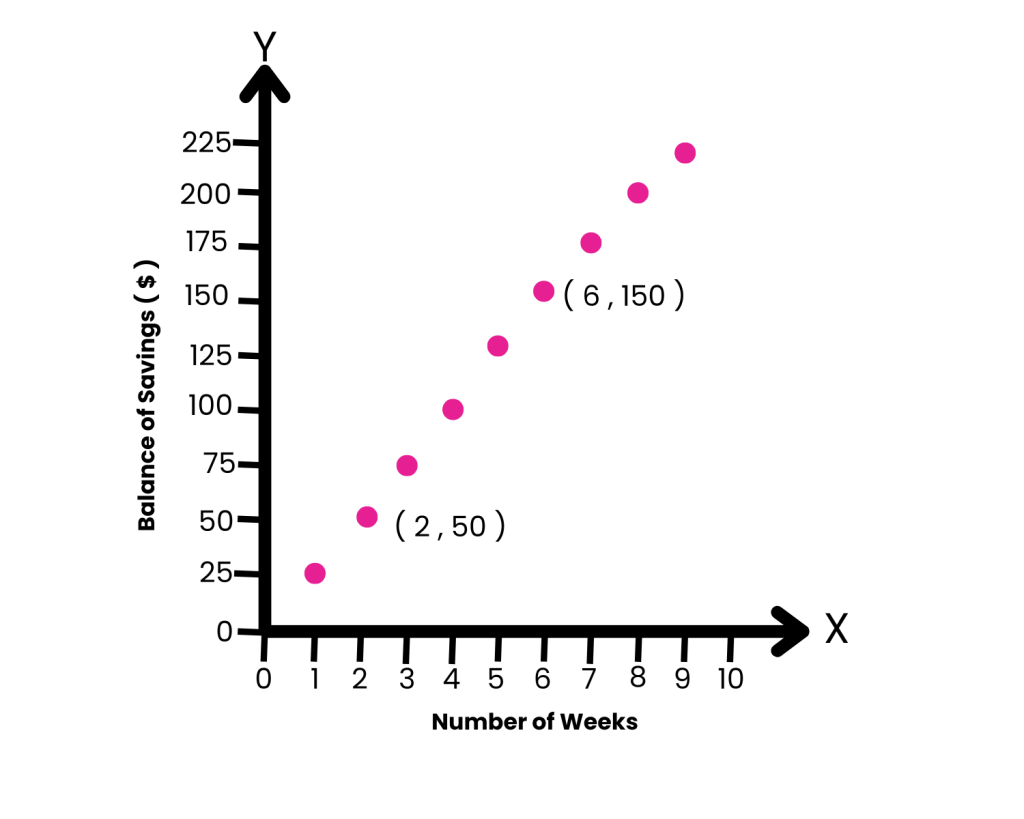
The equation for this graph is y = 25x + 0. (The line intersects the y-axis at 0.)

Expressions: Combinations of numbers, variables, and operations. Examples:

3x−1

-y

2(x−4)

Equations: Show relationships between expressions that are equal to each other. Examples:

2−y=20

8=x

3(x−1)=2(4x+5)

Inequalities: Show relationships between expressions that are not equal to each other. Examples:

8−4y <24x

x>4

2(x-10)≤ 3x +15

Other Graphs and Tables

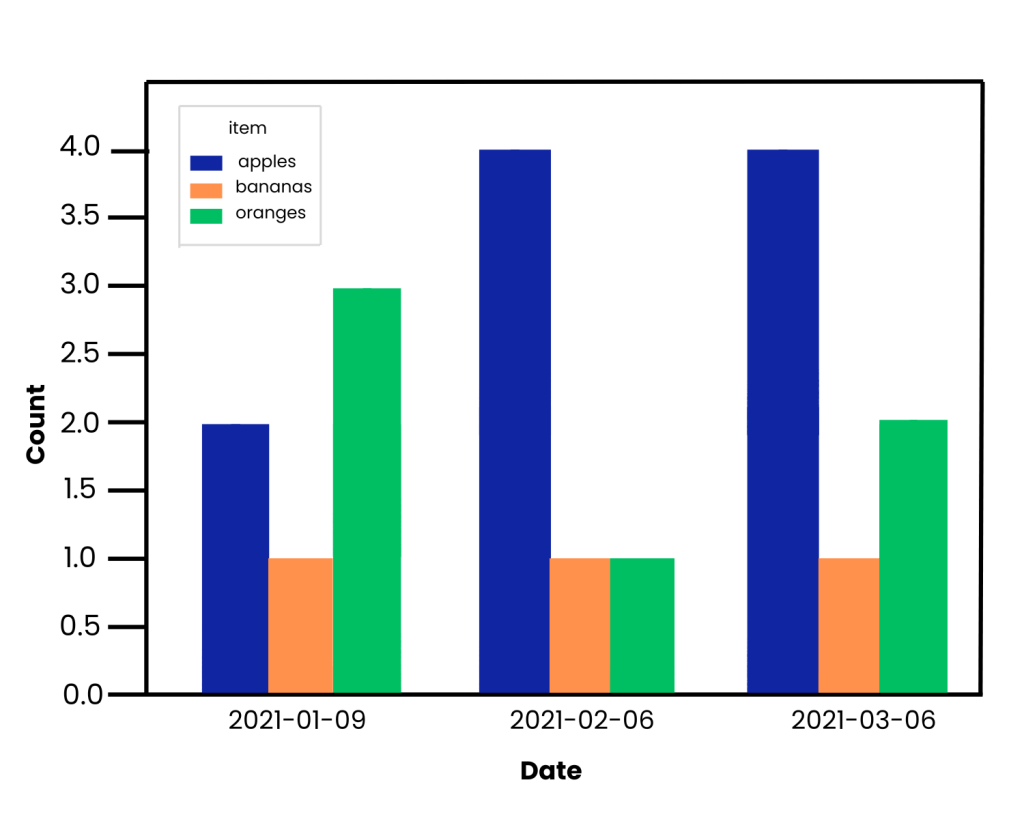
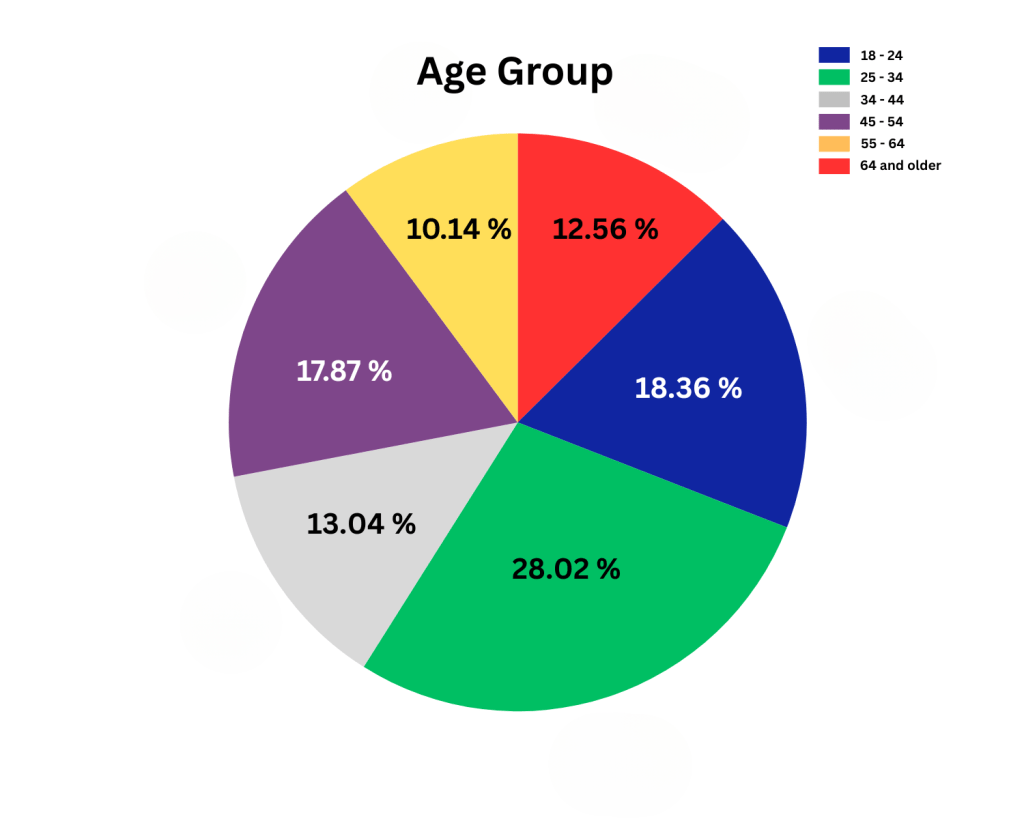
Evaluating Data

Mean: The average value of a data set. To calculate, sum all the values in the set and divide by the total number of values.

Median: The central value in a sorted list.
If the list has an odd number of items, there is a single median. If the list has an even number of items, there are two medians.

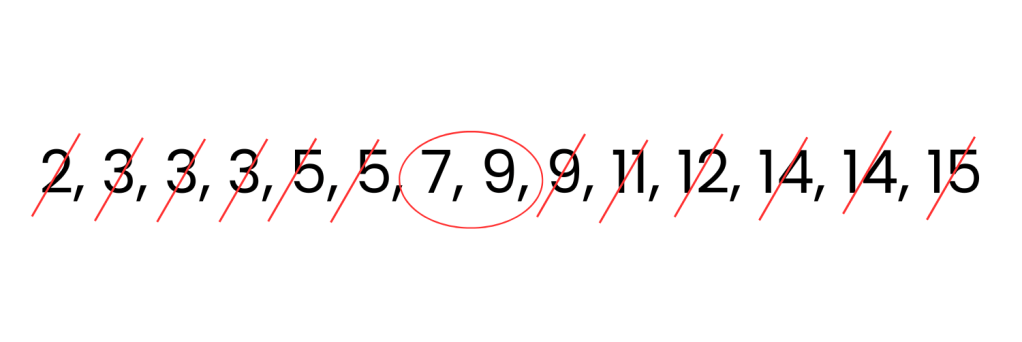
Mode: The value or values that appear most frequently in a data set.

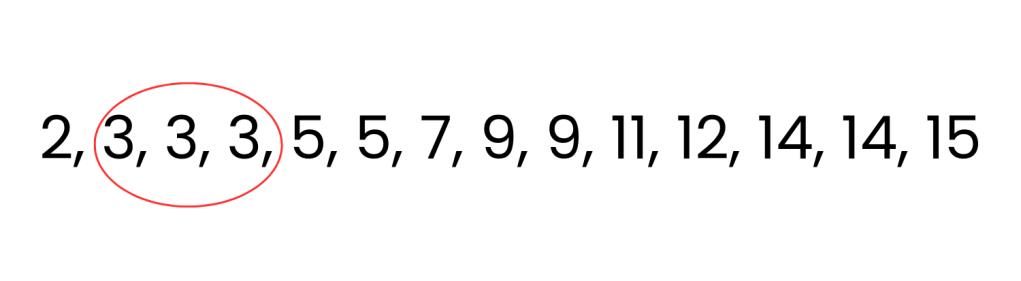
Range: The difference between the largest and smallest values in a data set. Find this by subtracting the smallest value from the largest.

Calculating Probability: To find the probability, divide the number of favorable outcomes by the total possible outcomes in the data set.

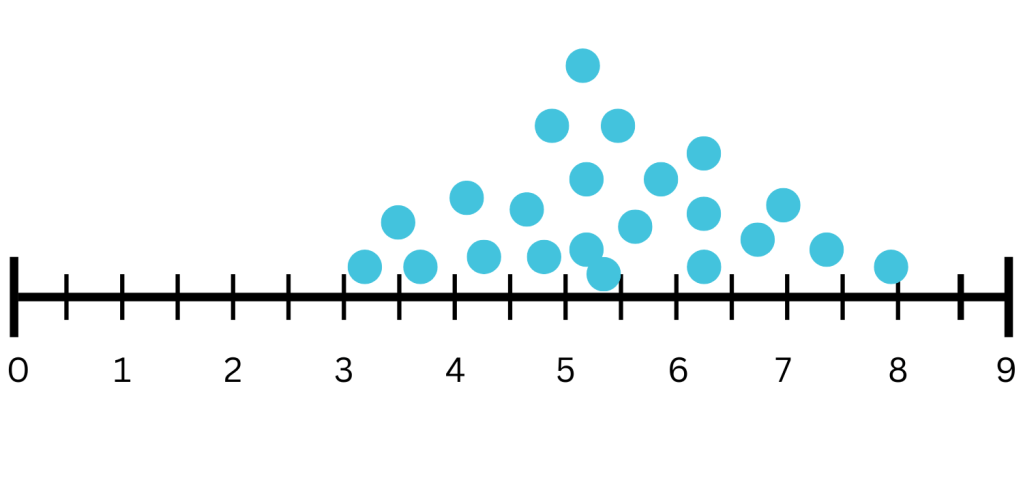
Distribution of Data

Symmetric Distribution: A type of data distribution where the plot is evenly divided at the center, with both halves being reflections of each other.

Unimodal: A distribution that has only one peak.
Bimodal: A distribution featuring two distinct peaks.
Skewed Left: A distribution where there are more values on the left side than the right.
Skewed Right: A distribution where there are more values on the right side than the left.
Uniform: A distribution where the data is evenly spread out, without any clear peaks.

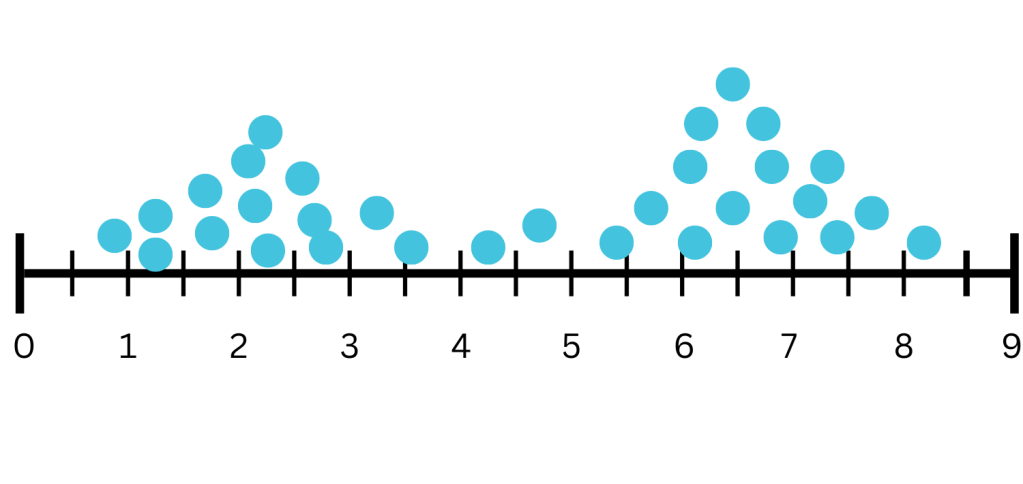
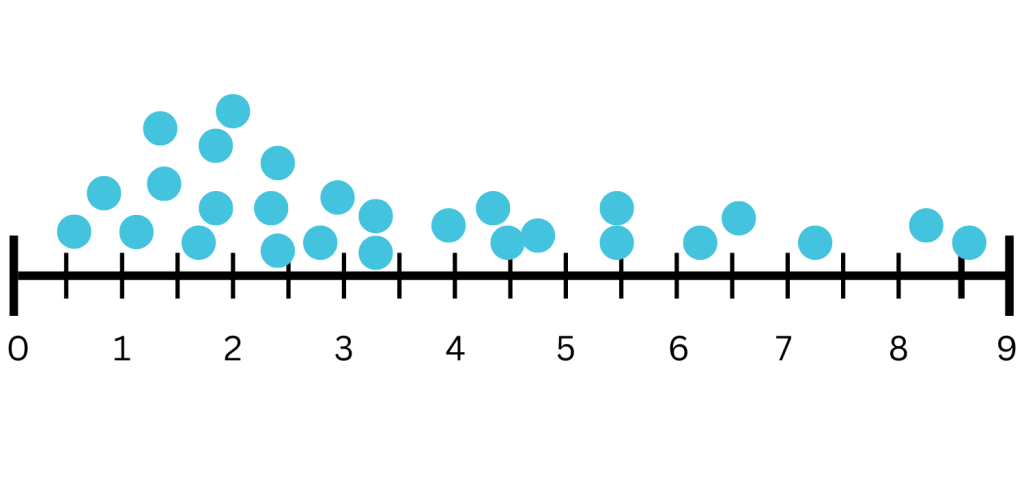
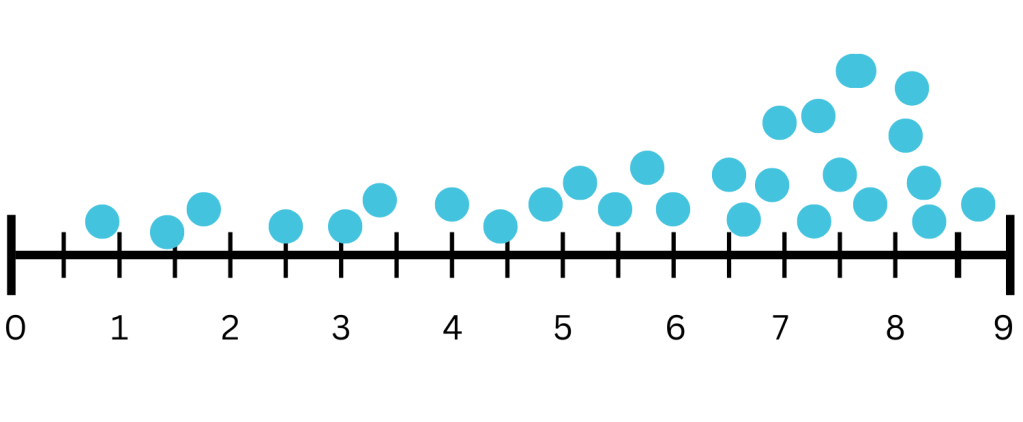
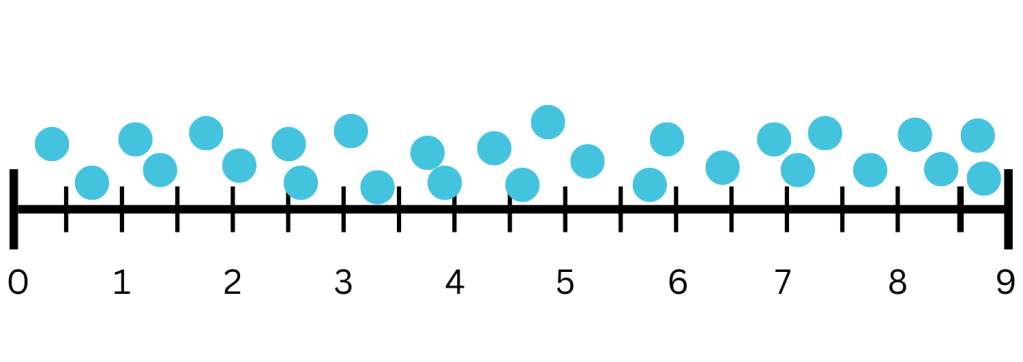
Perimeter and Area

Perimeter: The total length around a shape, calculated by adding the lengths of all its sides.

Circumference: The perimeter of a circle, representing the distance around it.

7 + 3 + 2 + 5 + 8 = 25 in
The length of the semi-circle can be determined using the formula C=πr
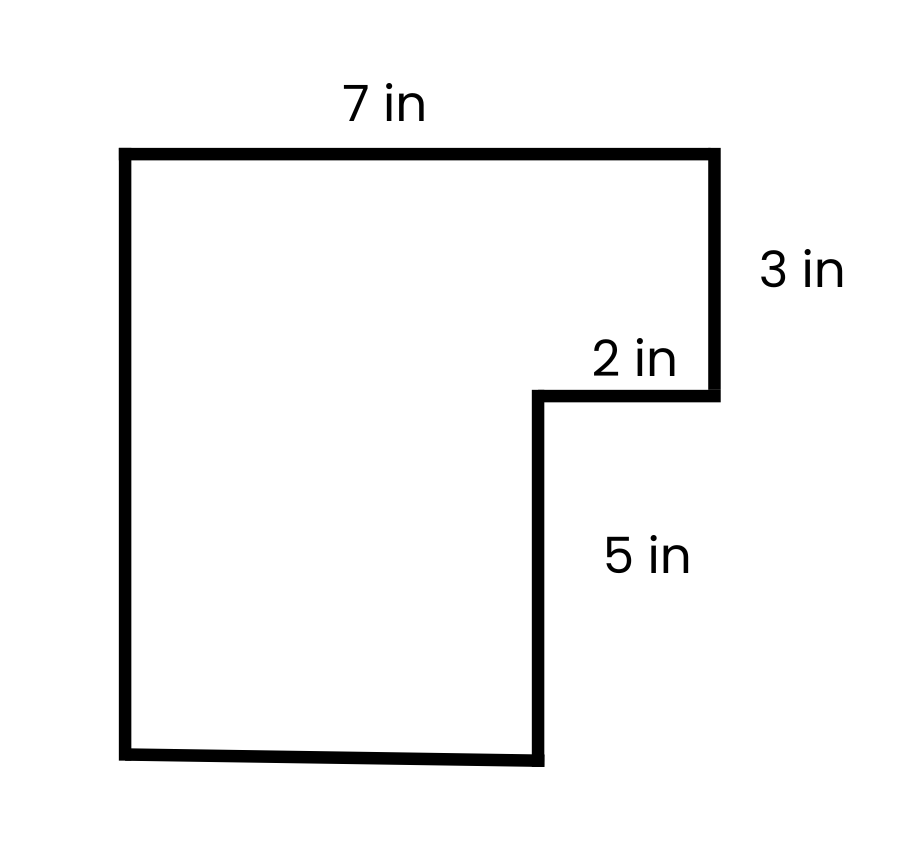
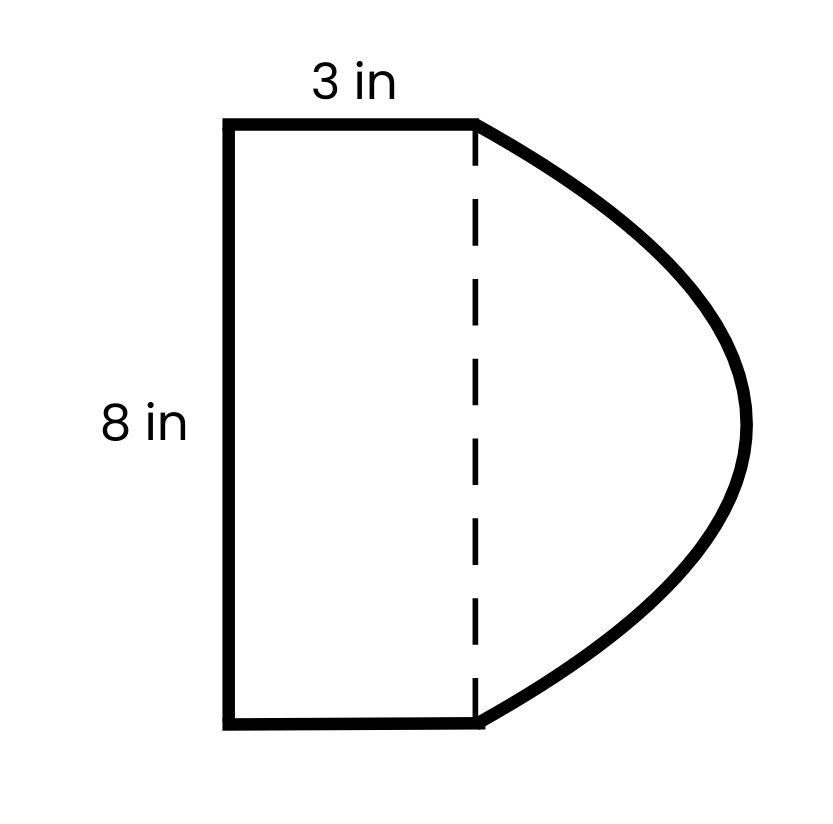
The radius is half of 8 in = 4in
π× 4 = 12.57
8 + 3 + 3 + 12.57 = 26.57 in
Circumference = perimeter of circle
C = 2πr Or C πD
D – Diameter = two times the radius
C = 2π4 = 25.13 in

Area: the amount of space a surface covers, typically measured in square units (in², cm², m²).

Formula: A = L × L = L²
A = 4 × 4 = 16 cm²
Formula: A = L x W
A = 6 × 3 = 18 cm²
Formula:
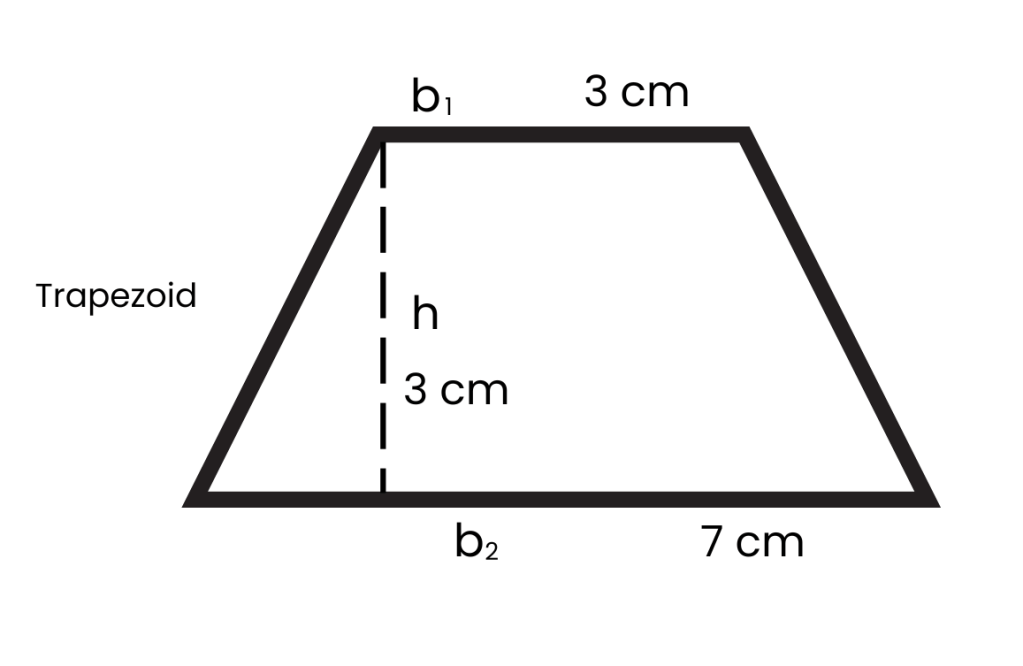
A = 1/2 × h × (b₁ + b₂)
A = 1/2 × 3 × (3 + 7) = 15 cm²
Formula:
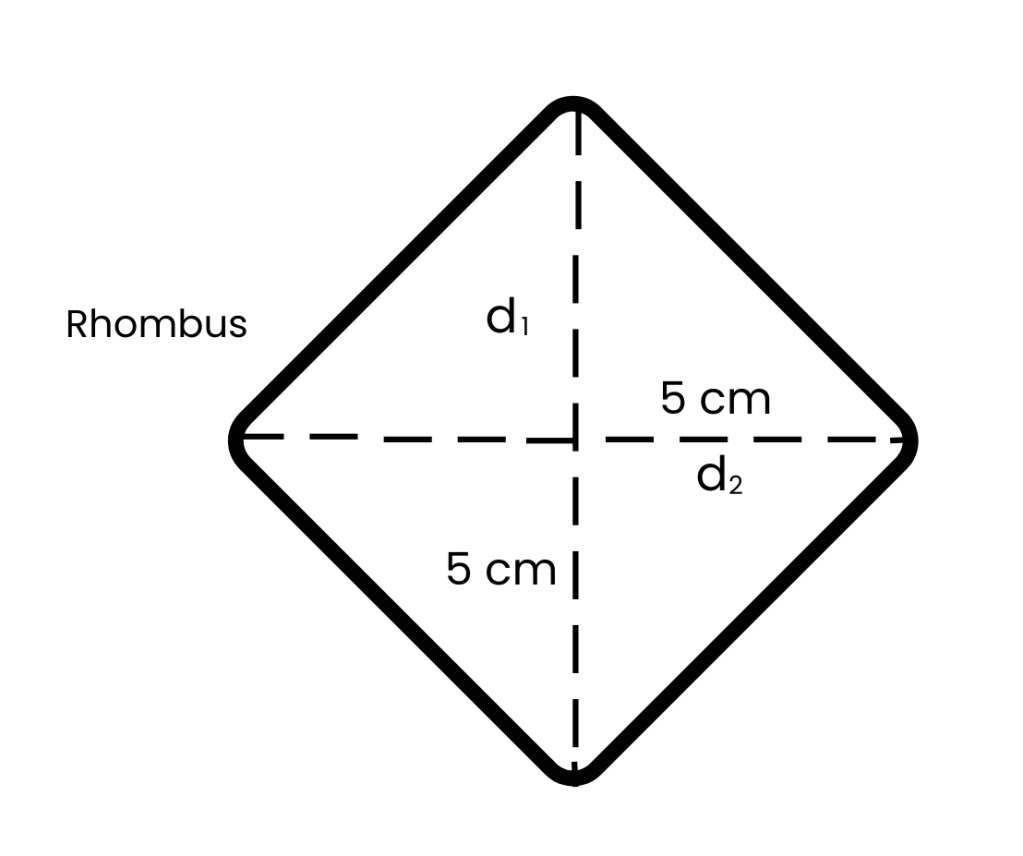
A = 1/2 × d₁ × d₂
A = 1/2 × (5 × 5) = 12.5 cm²
Formula:
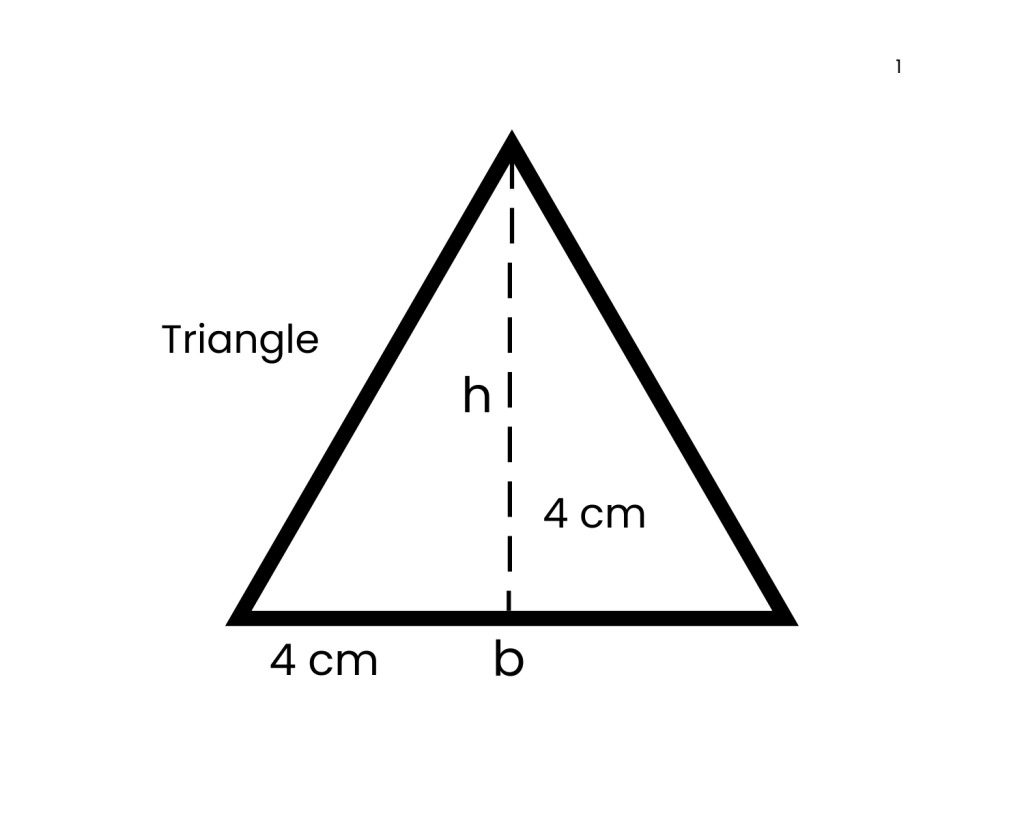
A = 1/2 b x h
A = 1/2 4 x r = 8 cm²
Formula:
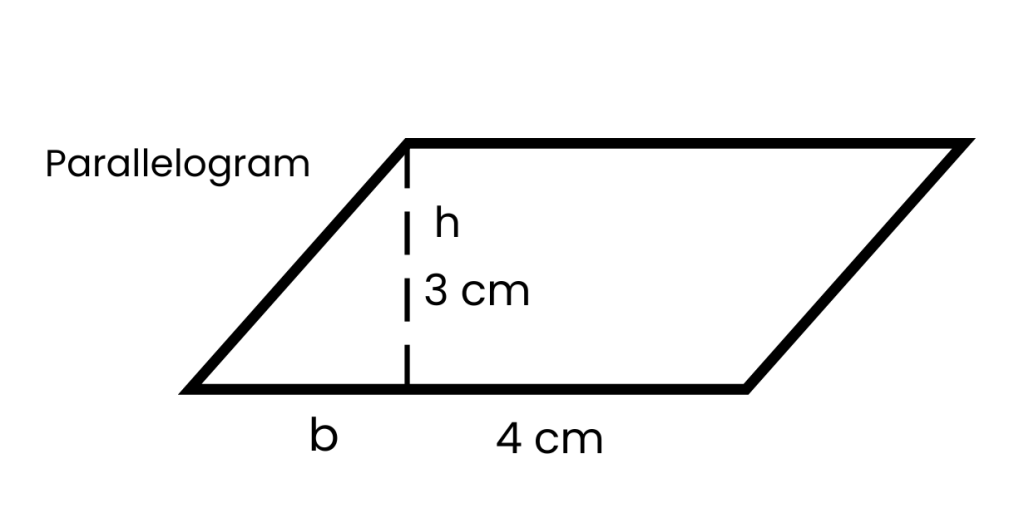
A = b x h
A = 4 x 3 = 12 cm²
Formula:
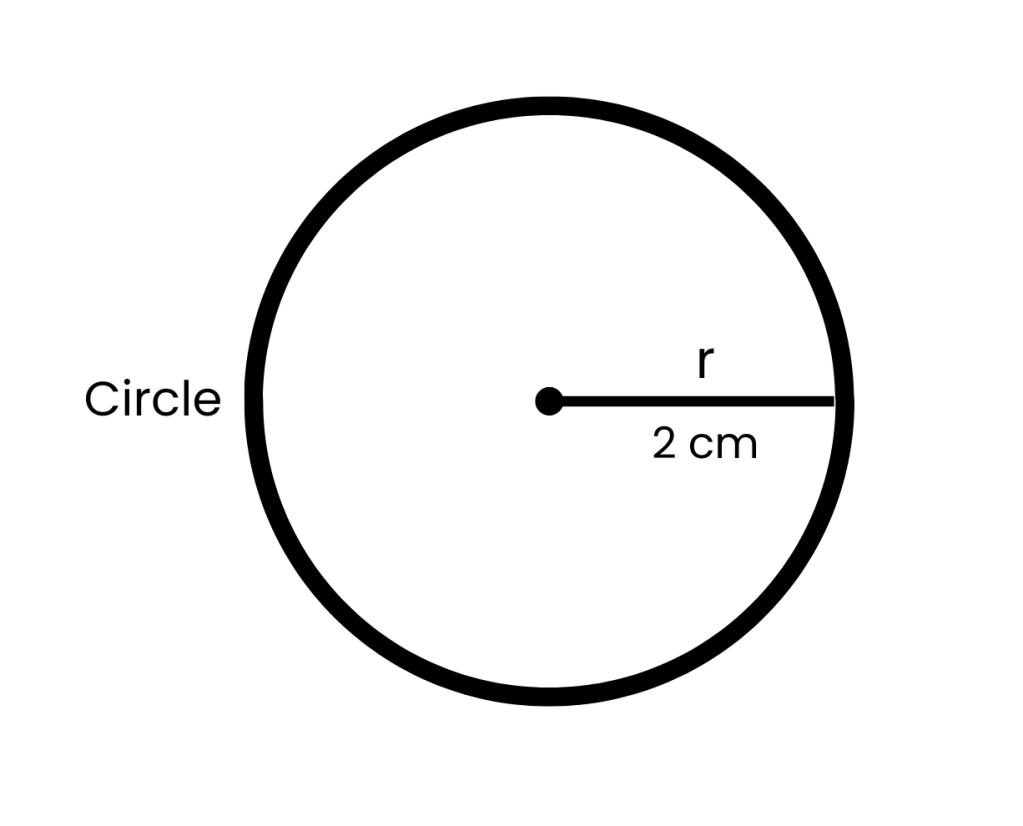
A = πr^2
A = π5^2 = 12.6 cm²
Formula:
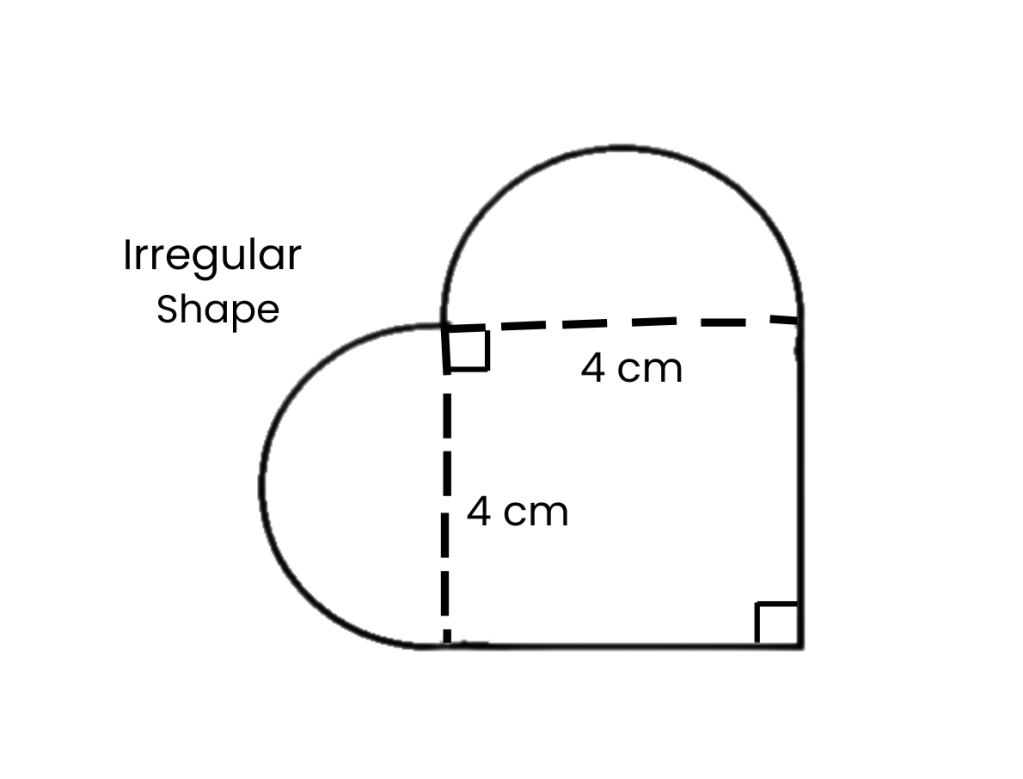
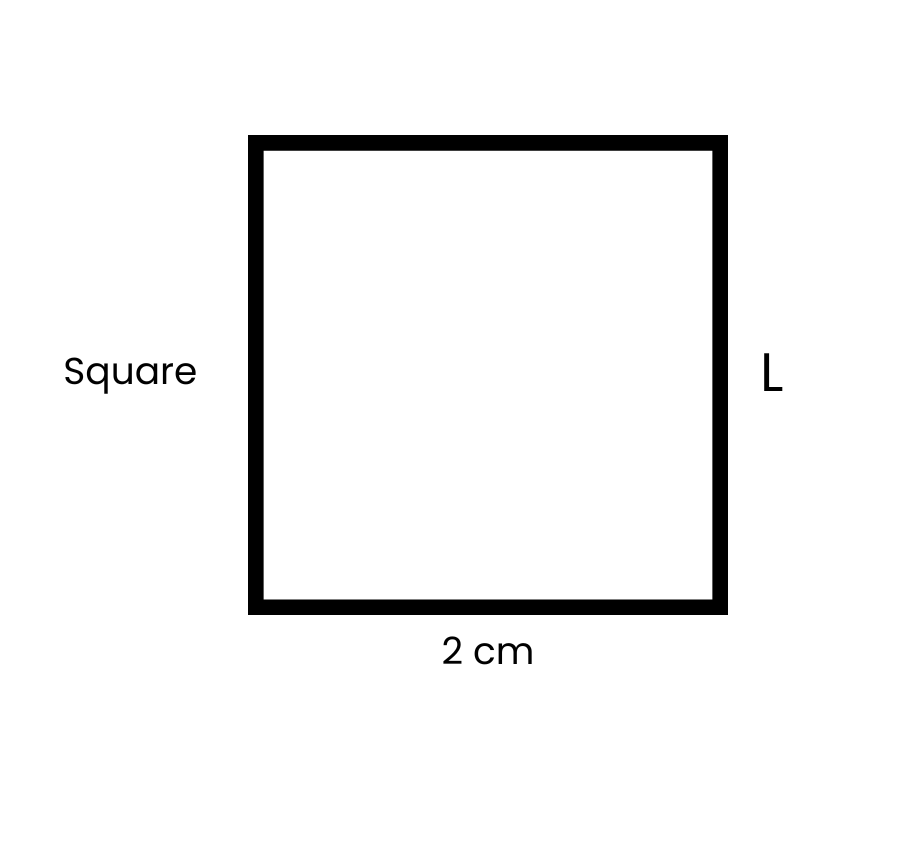
A = L × L
A = 4 x 4 = 16 cm²
Each semi circle:
A = (πr^2) ÷ 2
A = (πr^2) ÷ 2 = 6.3 cm²
6.3 + 6.3 + 16 = 28.6 cm²

Volume

Volume: The amount of space occupied by a 3D object
It is represented in cubic units such as (m³, cm³, in³).

Formula:
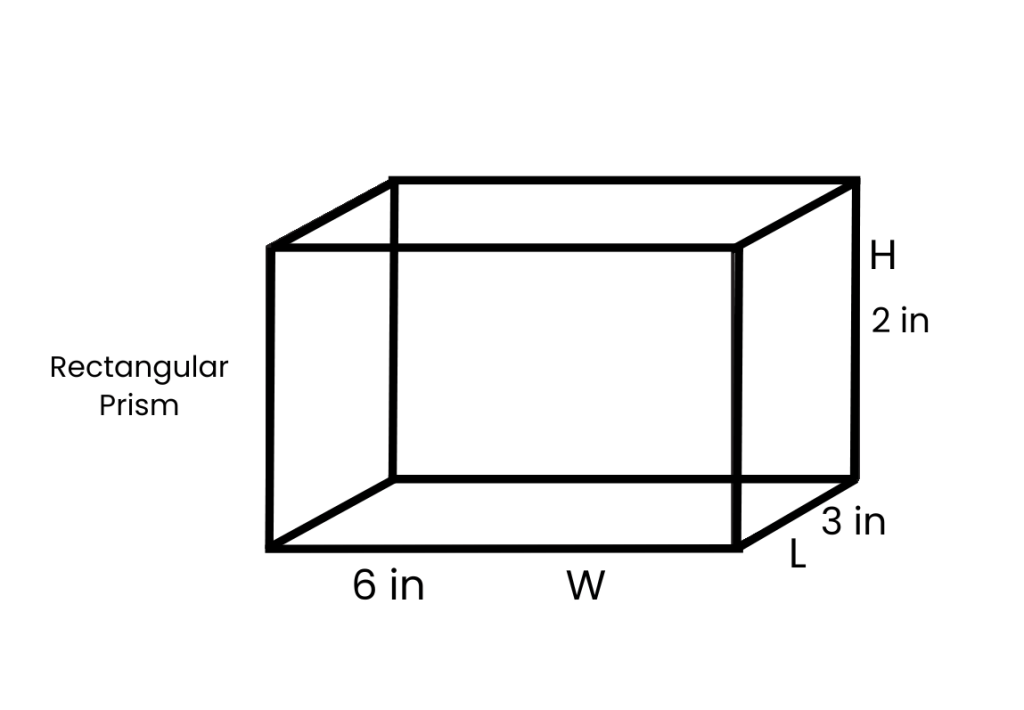
V – L x W x H
V = 3 x 6 x 2 = 36 in³
Formula:
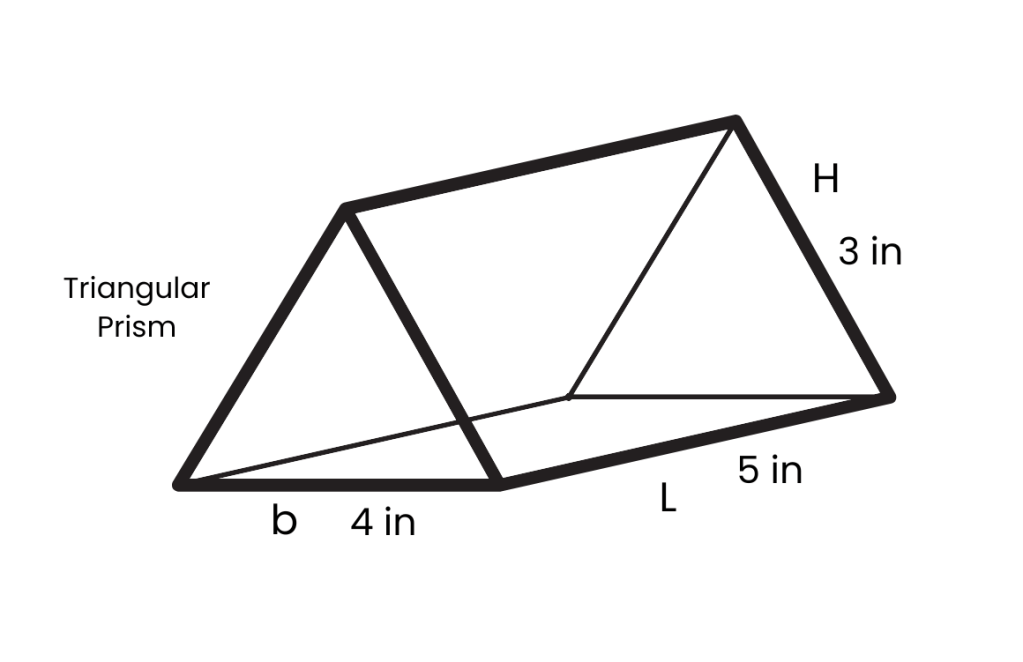
V = b x H x L / 2
V = 4 x 3 x 5 / 2 = 30 in³
Formula:
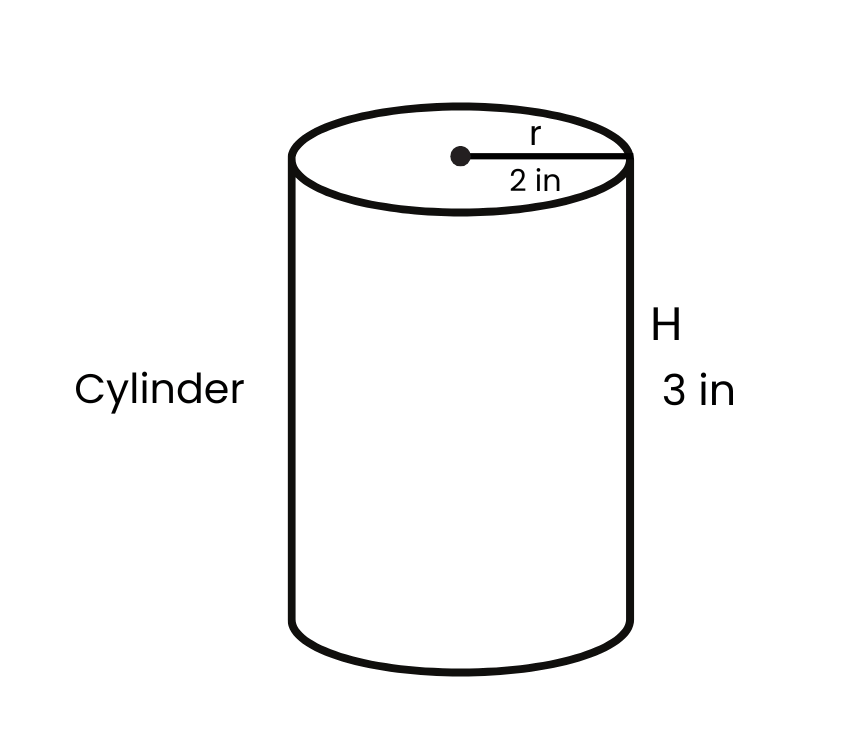
V = πr^2 h
V = π2^2 x 3 = 37.7 in³
Formula:
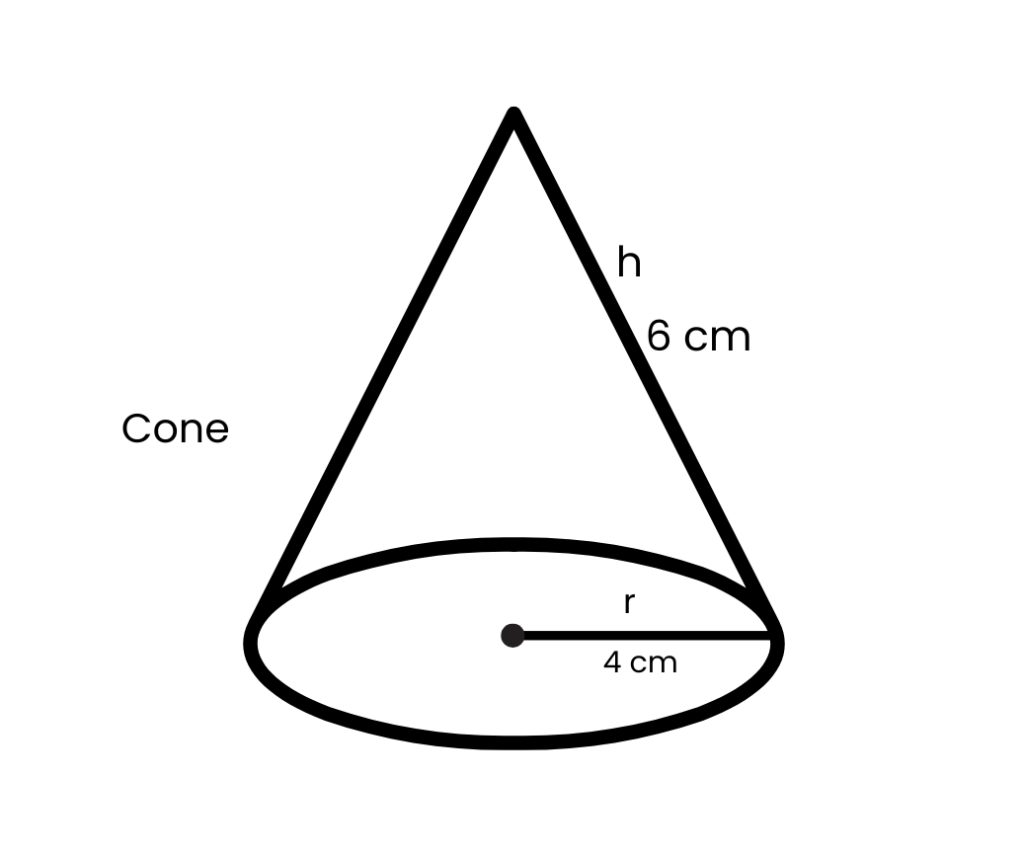
V = πr^2 h / 3
V = π4^2 x 6 / 3 = 100.5 in³
Formula:
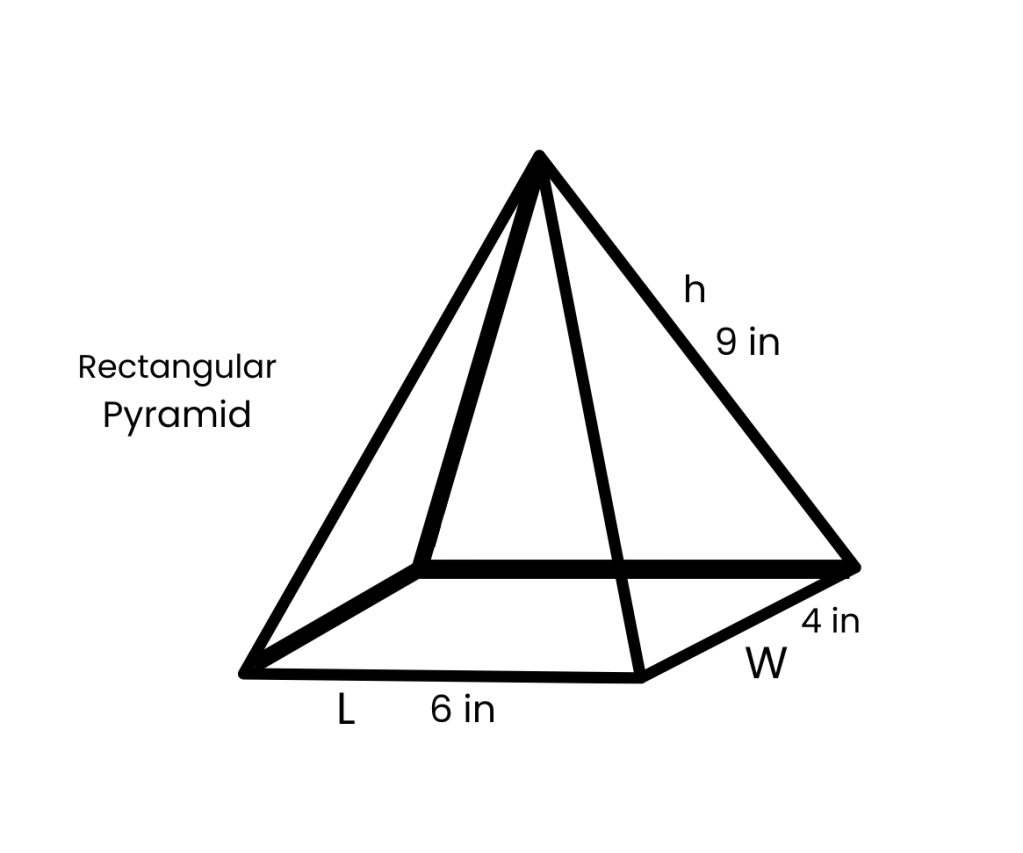
V = L x W x h / 3
V = 4 x 6 x 9 / 3 = 72 in³
Formula:
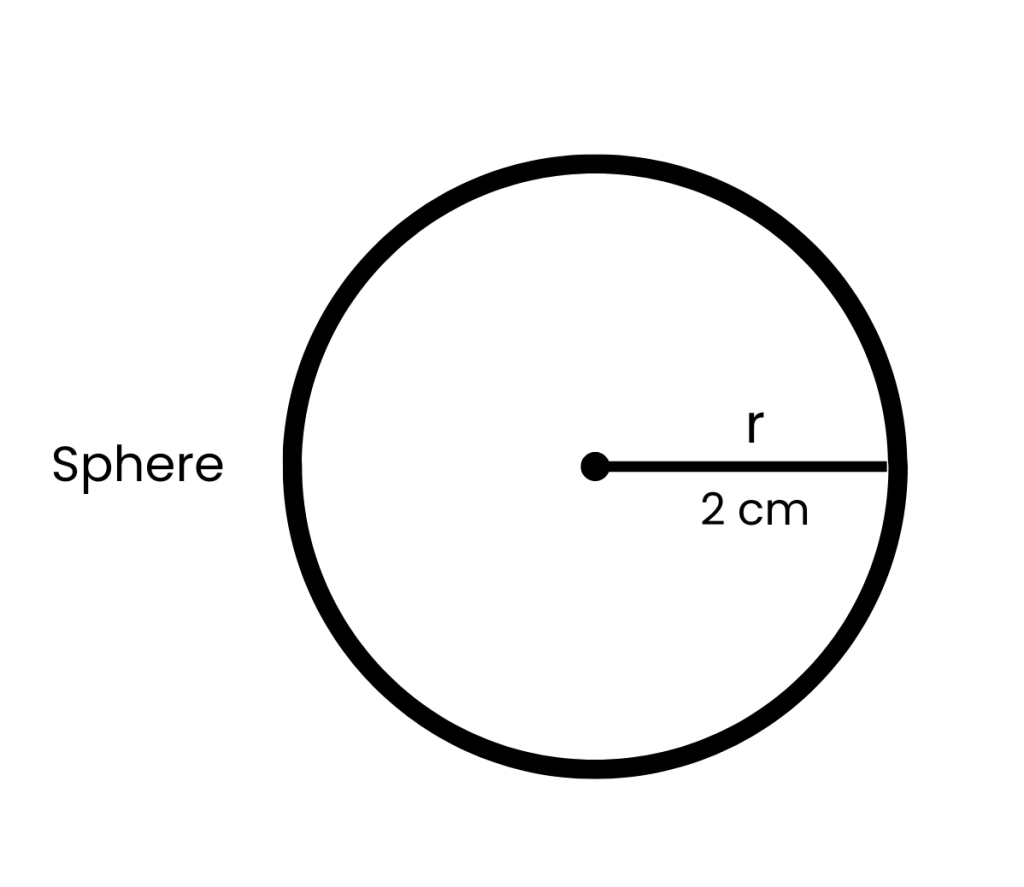
V = 4/3 πr^2
V = 4/3 π2^3 = 33.5 cm³

Posted

in

by

angelicasale08

Tags: