The Praxis Mathematics test measures a candidate’s ability to solve problems that reflect key mathematical principles. Some questions focus on individual concepts, while others may combine multiple ideas into a single scenario.
The problems generally avoid technical language, with the exception of basic terms like perimeter, area, integers, and ratios—these are considered foundational knowledge. Unless noted otherwise, diagrams are accurately drawn and positioned on a flat surface.
The exam questions fall into five main categories:
- Understanding Mathematical Concepts
These items test your grasp of core math ideas, particularly relating to numbers and basic operations. - Applying Mathematical Procedures
These questions deal with quantitative relationships and test your ability to interpret and carry out the steps needed to solve problems. - Interpreting Quantitative Data
These involve analyzing data, drawing logical conclusions from it, and identifying patterns or relationships within the data. - Measurement and Basic Geometry
These questions test knowledge of both standard (U.S.) and metric measurement systems, along with essential geometric concepts and properties. - Logical and Mathematical Reasoning
These items assess your use of logic to solve quantitative problems, evaluate arguments, and understand logical expressions.
Types of Numbers
Includes Integers, Odd & Even Values, Prime Numbers, and Digits
- Integers:
A collection of whole numbers that may be positive, negative, or zero.
Example: …, -4, -3, -2, -1, 0, 1, 2, 3, 4, … - Consecutive Integers:
Whole numbers that come one after another without gaps.
Example: 22, 23, 24, 25
These can be written generally as: n, n + 1, n + 2, n + 3, and so on. - Odd Numbers:
Numbers that are not divisible evenly by 2.
Example: …, -9, -7, -5, -3, -1, 1, 3, 5, 7, 9, … - Even Numbers:
Values that divide evenly by 2, including both positive and negative numbers.
Example: …, -8, -6, -4, -2, 0, 2, 4, 6, 8, …
(Remember: 0 is classified as an even number.) - Prime Numbers:
Numbers greater than 1 that are divisible only by 1 and themselves.
Example: 2, 3, 5, 7, 11, 13, 17, 19, …
(Note: 1 is not prime, and 2 is the only even number that is prime.) - Digits:
The ten basic symbols used to create all numbers in our number system:
0, 1, 2, 3, 4, 5, 6, 7, 8, 9
Addition and Multiplication of Even and Odd Numbers
| Operation Type | Expression | Result |
|---|---|---|
| Addition | even + even | equals even |
| Addition | odd + odd | results in even |
| Addition | even + odd | gives an odd number |
| Multiplication | even × even | results in even |
| Multiplication | even × odd | equals even |
| Multiplication | odd × odd | gives an odd number |
Understanding Percentages
Percent literally means “per hundred,” or a portion out of 100. For instance, saying 40 percent is the same as saying 40 out of 100, which can be written as the fraction 40/100, the decimal 0.40, or simplified to 2/5.
When Percent is Less Than 100
Example 1:
A $30 product includes a sales tax of $1.80. What is the tax rate applied?
Solution:
Use the equation:
1.80 = (rate/100) × 30
Solving gives: rate = 6, so the sales tax is 6%.
When Percent is More Than 100
Example 2:
What is 250% of the number 2?
Solution:
Value = (250/100) × 2 = 5,
So, the result is 5.
When Percent is Less Than 1
Example 3:
The number 3 is 0.2% of what total amount?
Solution:
Set up the equation:
3 = (0.2/100) × total
Solving gives: total = 1,500,
So, 3 is 0.2% of 1,500.
Calculating Percentage Change
Example 4:
The cost of a computer dropped from $1,000 to $750. What percentage does this drop represent?
Solution:
The price dropped by $250.
Now, use the formula:
Change ÷ Original = Percent Change ÷ 100
So, 250 ÷ 1000 = percent ÷ 100 → percent = 25
This means there was a 25% decrease.
Helpful Tip:
- To find a percent increase:
(increase÷original)=percent÷100(increase ÷ original) = percent ÷ 100(increase÷original)=percent÷100 - To find a percent decrease:
(decrease÷original)=percent÷100(decrease ÷ original) = percent ÷ 100(decrease÷original)=percent÷100
Averages and Measures of Central Tendency
One method of summarizing a data set is by calculating an average. The most common type of average is the arithmetic mean, which is found by adding all the values in a group and dividing the result by the total number of values. For example, to find the average of 2, 3, 5, 7, and 13:
(2+3+5+7+13)÷5=30÷5=6(2 + 3 + 5 + 7 + 13) ÷ 5 = 30 ÷ 5 = 6(2+3+5+7+13)÷5=30÷5=6
If you’re given the average of a group and know how many numbers are in the list, you can calculate the total. For instance, if six numbers have an average of 12, their total is: 12×6=7212 × 6 = 7212×6=72
When a list is ordered from smallest to largest or vice versa, the middle number is known as the median. Take this unordered list: 3, 8, 2, 6, 9. When arranged in order: 2, 3, 6, 8, 9 — the center value is 6, so that’s the median.
If a list has an even number of values, the median is found by averaging the two middle numbers. For example, for the numbers 6, 8, 9, 13, 14, and 16, the two center numbers are 9 and 13: (9+13)÷2=11(9 + 13) ÷ 2 = 11(9+13)÷2=11
The mode refers to the number that shows up most frequently in a group. In the set 2, 7, 5, 8, 7, 12, the value 7 occurs more than any other, so it’s the mode. A set can have more than one mode (bimodal), like 2, 4, 2, 8, 2, 4, 7, 4, 9, 11 — which has both 2 and 4 as modes. It’s also possible to have no mode at all, such as in the list 10, 12, 14, 16, 18, where no number repeats.
Keep in mind: mean, median, and mode all represent different types of averages. On most questions, if you see “average (arithmetic mean),” it specifically refers to the mean. One exception is when you’re solving for average speed, which follows a different formula. If a question is about the median or mode, the test will clearly mention those terms.
Weighted Average
Problem 1: There are 10 students in a group: 7 students are 13 years old, and 3 students are 17 years old. What is the mean age of all 10 students combined?
Solution: The answer is not simply the midpoint between 13 and 17, which would be 15. Instead, the mean is calculated by taking into account the number of students at each age:
(7 × 13 + 3 × 17) ÷ 10 = (91 + 51) ÷ 10 = 14.2 years
This is called a “weighted average” because the number 13 is multiplied by its count of 7 (the weight), and 17 is multiplied by its count of 3 (its weight).
Average Speed
Problem 2: Jane drove for 2 hours at 70 km/h and then for 5 hours at 60 km/h. What was her overall average speed during the entire 7-hour trip?
Solution: The average speed here is the total distance divided by the total time. The total distance traveled is:
(2 × 70) + (5 × 60) = 440 km
The total time is 7 hours, so the average speed is:
440 ÷ 7 ≈ 62.86 km/h
Note that this average speed is different from simply averaging the two speeds (which would be 65 km/h).
Properties of Signed Numbers
- Positive × Negative = Negative
- Negative × Negative = Positive
- Negative × Positive = Negative
- Positive × Positive = Positive
Factoring
Here are some common factoring forms you might use:
- x²+2x can be factored as x(x+2)x(x + 2)x(x+2)
- x²−1 factors into (x+1)(x−1)(x + 1)(x – 1)(x+1)(x−1)
- x²+2x+1 breaks down to (x+1)(x+1)(x + 1)(x + 1)(x+1)(x+1), which is the same as (x+1)2(x + 1)^2(x+1)²
- x²x2−3x−4 factors as (x−4)(x+1)(x – 4)(x + 1)(x−4)(x+1)
Probability
Probability tells us how likely it is that a certain event will happen. When all possible outcomes have the same chance, probability is found by this formula:
Probability = (Number of favorable outcomes) ÷ (Total number of possible outcomes)
For example, if a jar has 7 green marbles and 13 red marbles, the chance of picking a green marble at random is:
7 ÷ (7 + 13) = 7 ÷ 20 = 0.35
If an event cannot happen, its probability is 0. If an event will definitely happen, its probability is 1. Usually, probability values (called p) are between 0 and 1. Probability can be shown as a fraction or a decimal.
Geometric Figures
The diagrams included with problems provide details that help in solving them. Unless a problem specifically states that the figure is not drawn to scale, the diagrams are shown as accurately as possible. In general, you can assume the order of points and angles shown is correct, even if the figure isn’t perfectly to scale. Also, if line segments look like they lie on the same straight line and pass through points, you can assume they are on the same line. Sometimes, lengths and angle measurements might not be shown exactly right; in these cases, the test will include a note saying “Figure not drawn to scale.” Below are examples that show how different figures can be interpreted.
Example 1
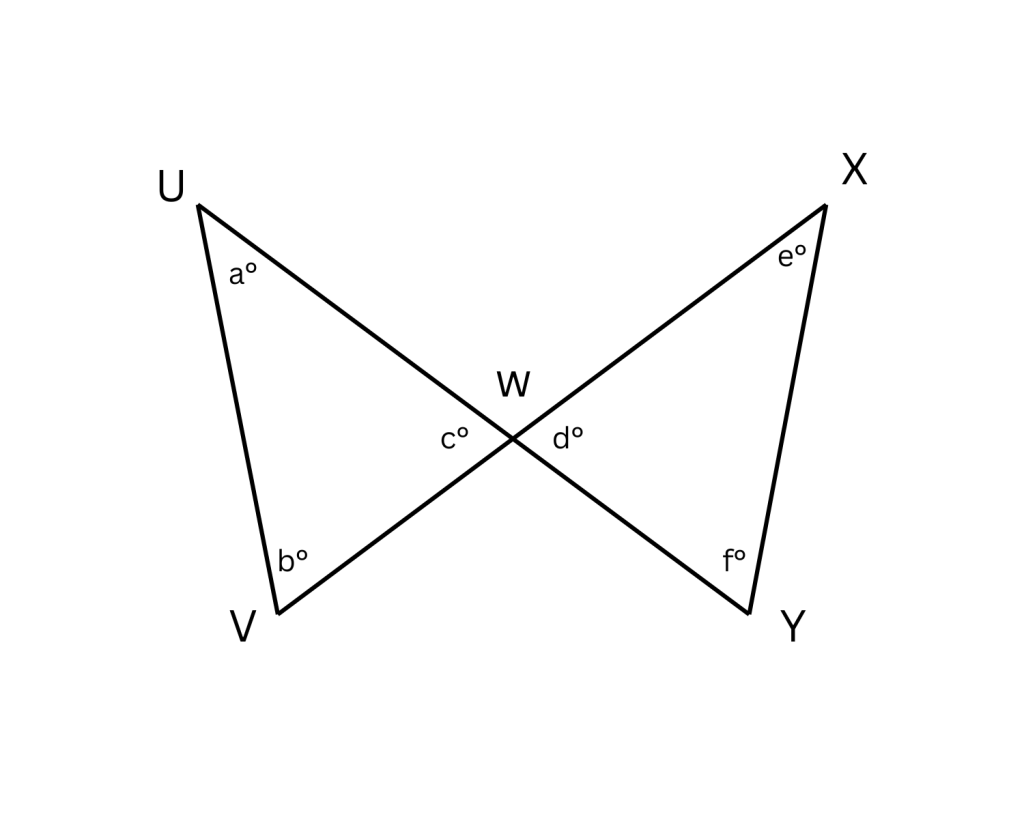
Since UY and VX are line segments, angles UWV and XWY are vertical angles. This means you can conclude that c=d. Even though the figure is drawn to scale, do not make any other assumptions without additional information. For example, although some angles might look like right angles in the drawing, you should not assume that VW=WY or that the angle at vertex Y is a right angle.
Example 2
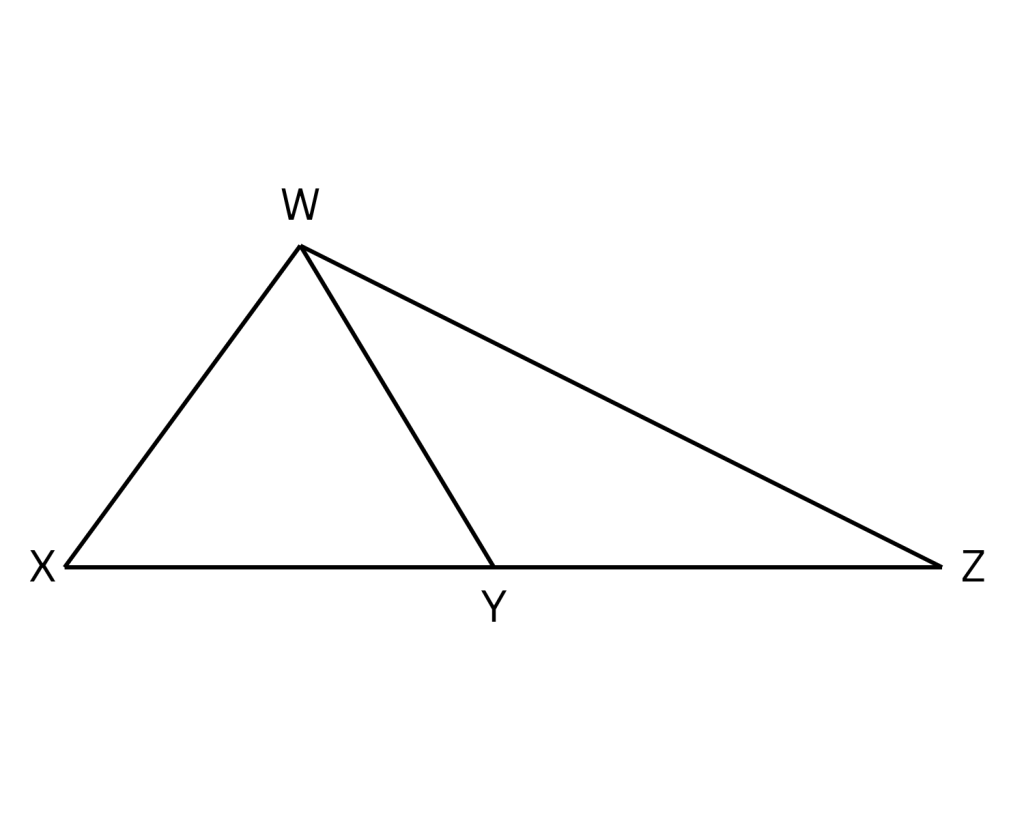
A triangle such as XWZ might appear in a question. Even if the diagram includes a note saying it’s not drawn to scale, you can reasonably assume the following:
- XWY and YWZ are both triangles.
- Point Y lies between points X and Z.
- X, Y, and Z are collinear (on the same straight line).
- Segment XY is shorter than segment XZ.
- Angle XWY is smaller than angle XWZ.
However, you should not make the following assumptions unless stated:
- That XY is shorter than YZ.
- That angles WXY and WYX have equal measures.
- That angle XWY is larger than angle WYX.
- That angle XWZ is a right angle.
Geometric Skills and Concepts
Properties of Parallel Lines
- When a transversal intersects two parallel lines, the alternate interior angles are congruent (equal in measure).
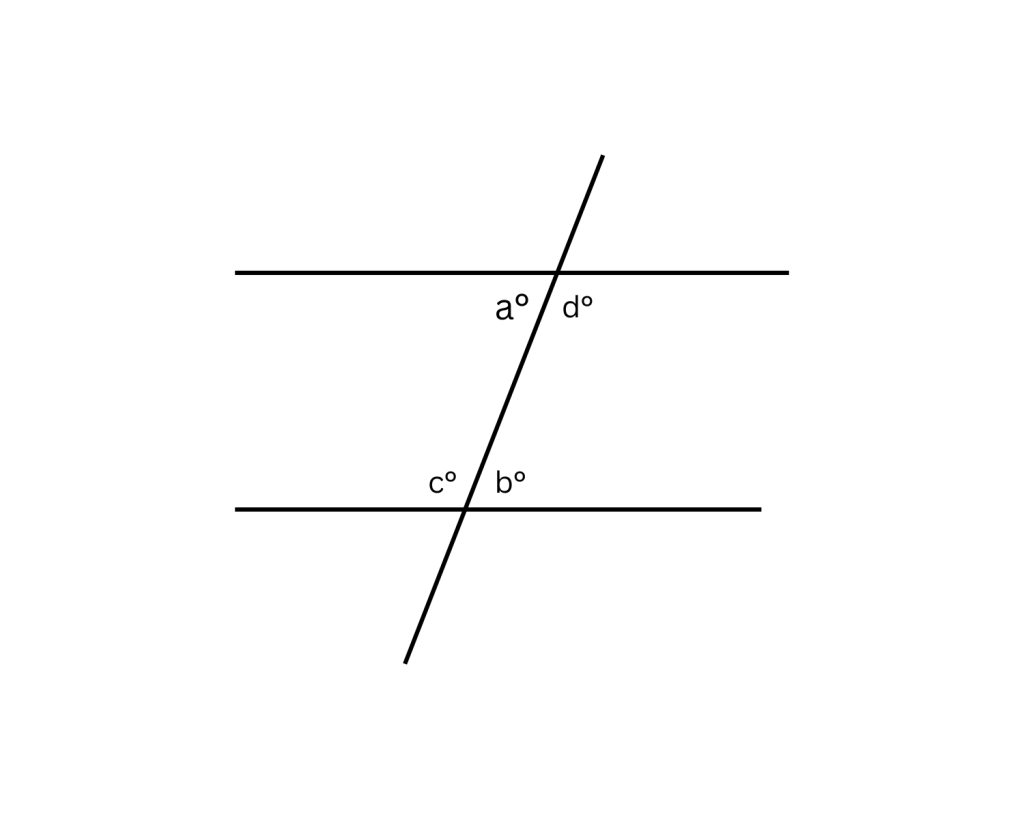
2. If a transversal intersects two parallel lines, the angles that occupy the same relative position at each intersection point are equal in measure.
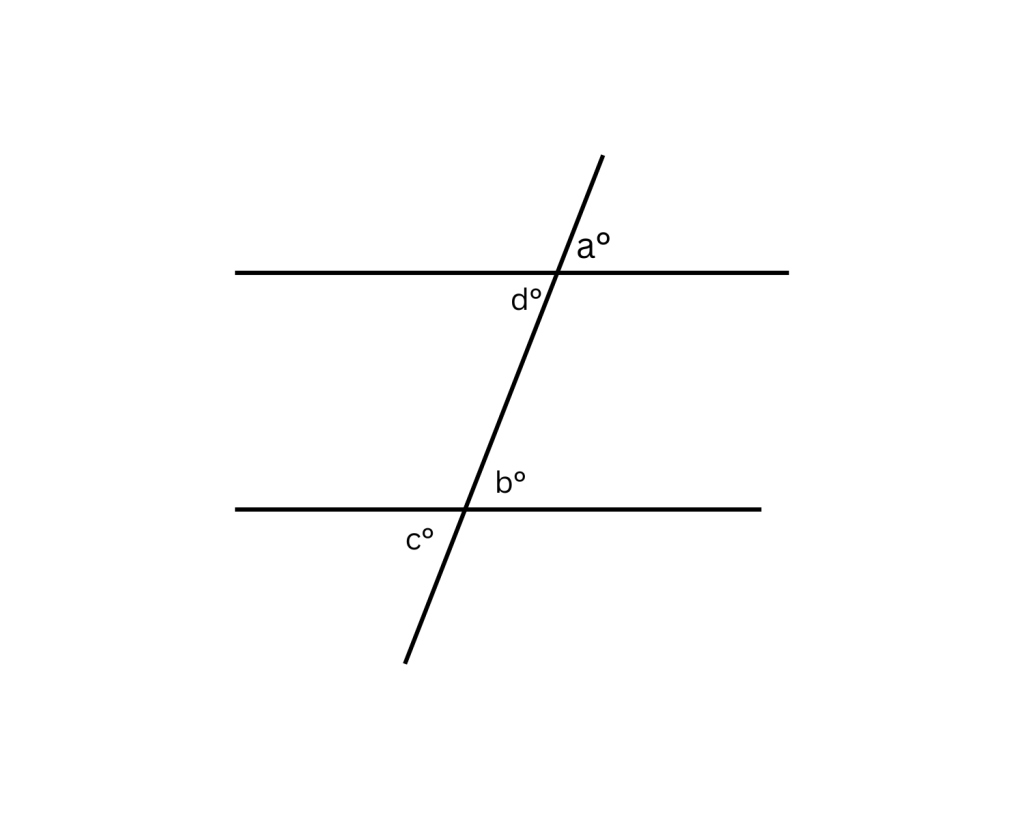
Note: The test typically avoids terms like “alternate interior” or “corresponding,” but you still need to recognize which angles formed by parallel lines and a transversal are equal.
3. When two parallel lines are intersected by another line, the two interior angles on the same side of the intersecting line always add up to 180 degrees.
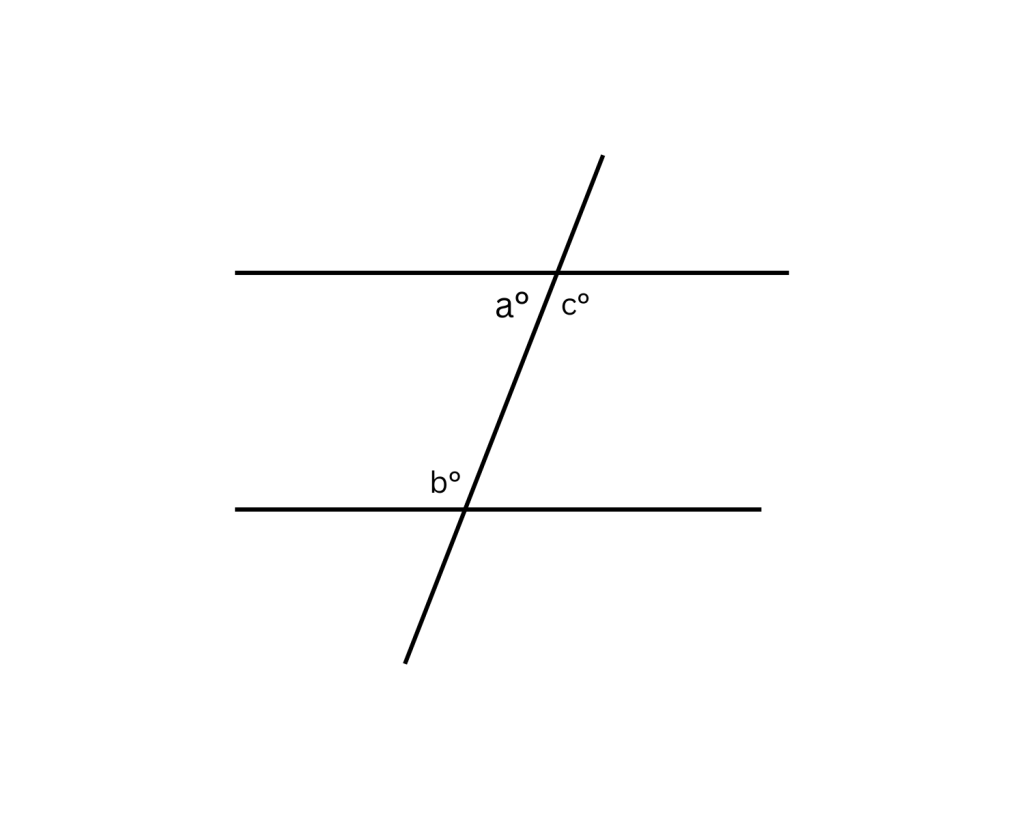
Angle Relationships
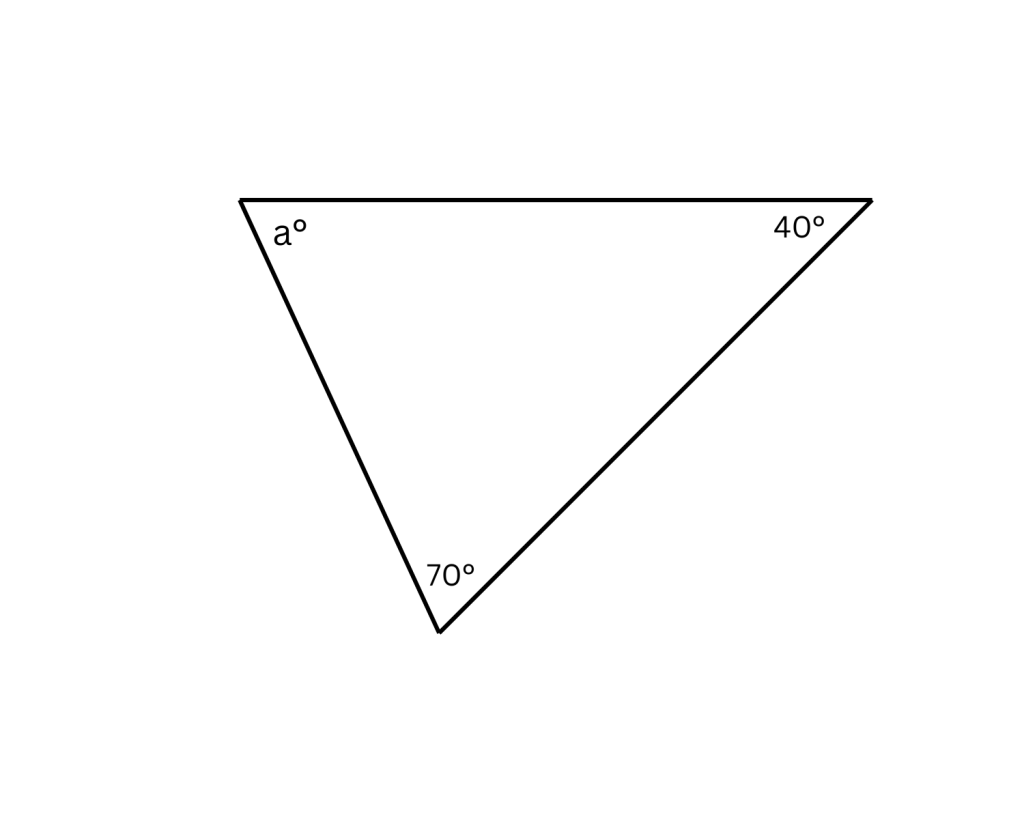
- The sum of all interior angles in a triangle is always 180 degrees.
2. When two lines cross, the opposite (vertical) angles formed at their intersection are always equal.
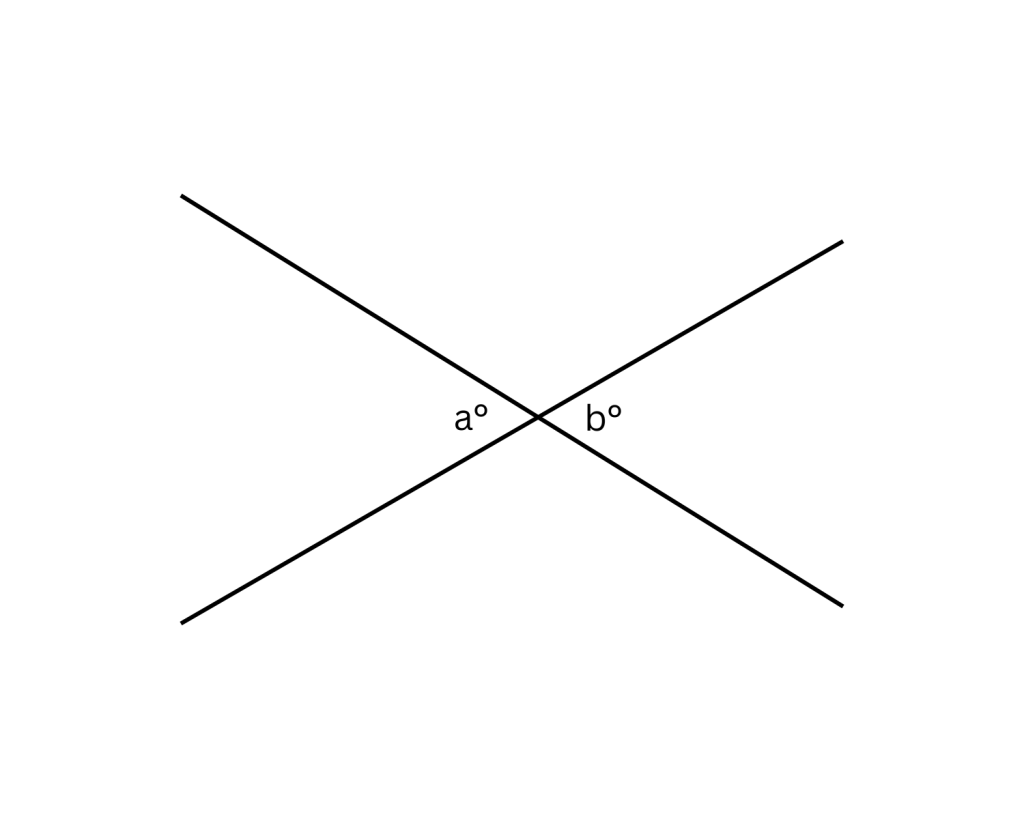
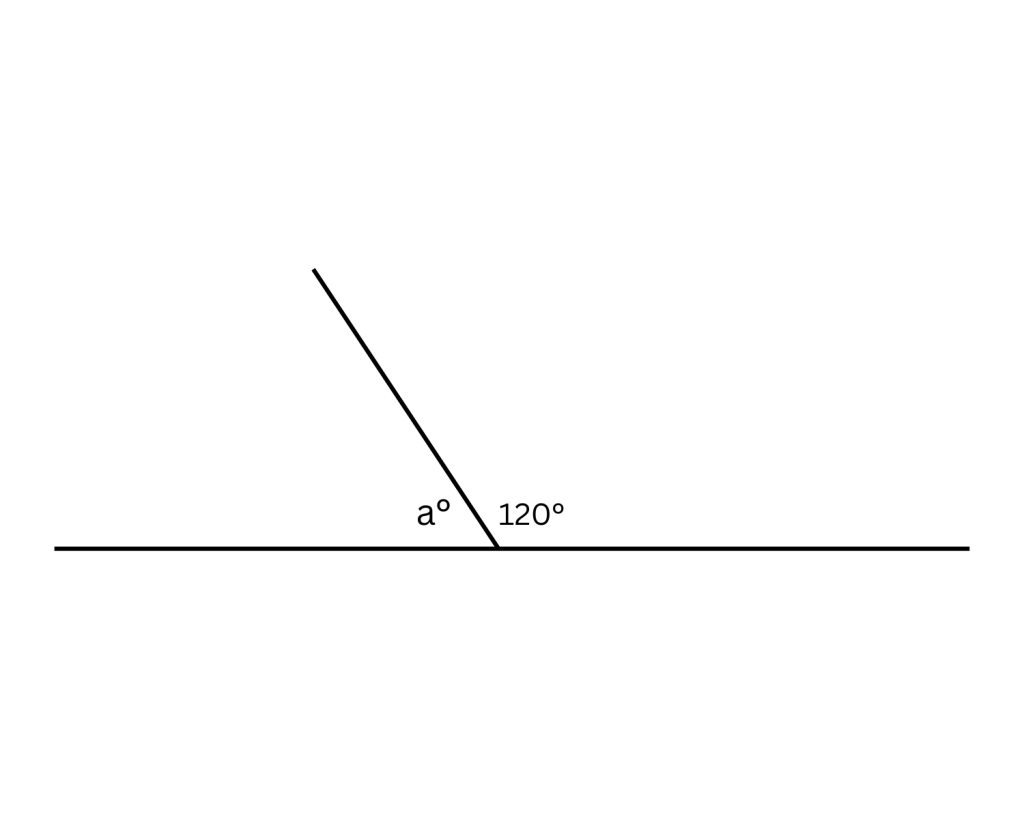
3. A straight angle has a measure of exactly 180 degrees.
4. In a right triangle, the sum of the two non-right (acute) angles is 90 degrees.
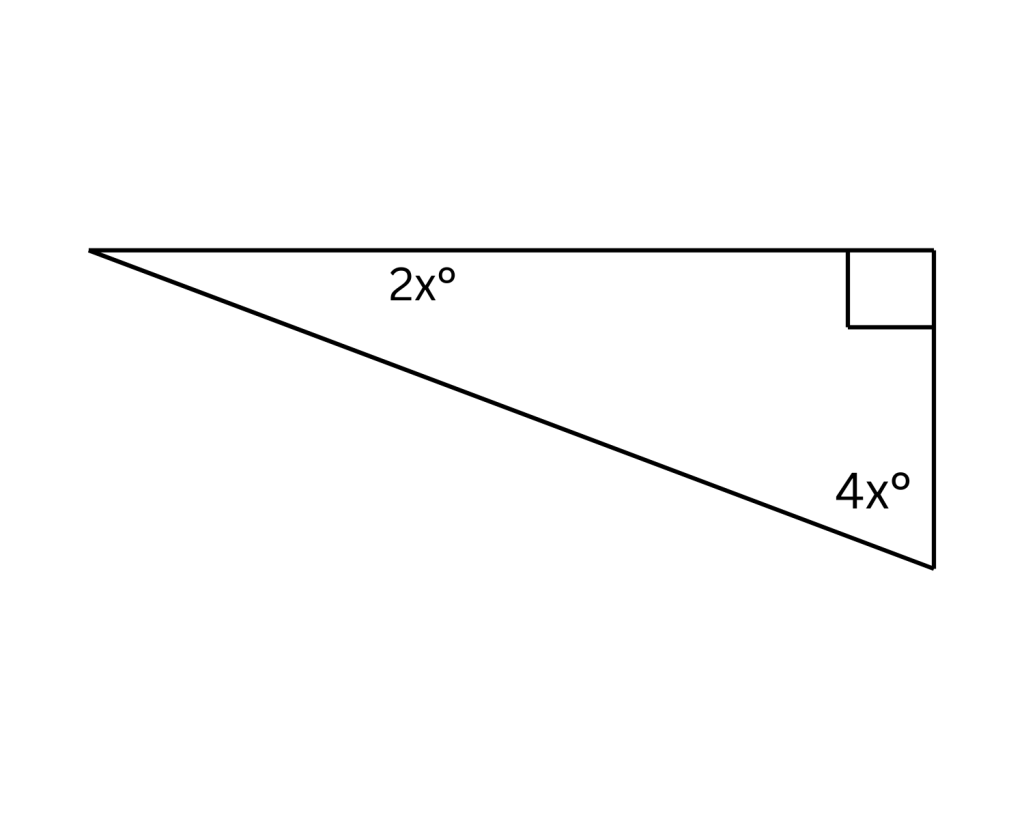
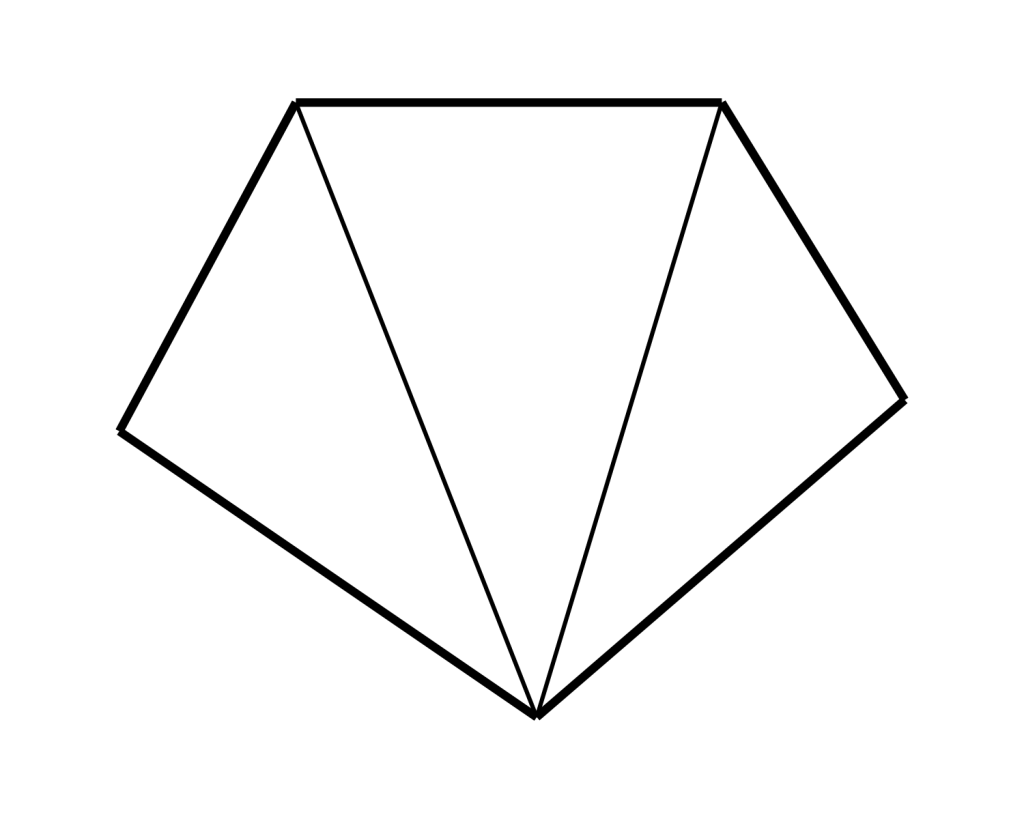
5. You can calculate the sum of a polygon’s interior angles by drawing all possible diagonals from one vertex, counting the number of triangles formed, and then multiplying that number by 180 degrees.
Side Relationships
1. Pythagorean Theorem: In a right triangle, the sum of the squares of the two shorter sides is equal to the square of the longest side, represented as:
a² + b² = c², where c is the hypotenuse and a and b are the legs.
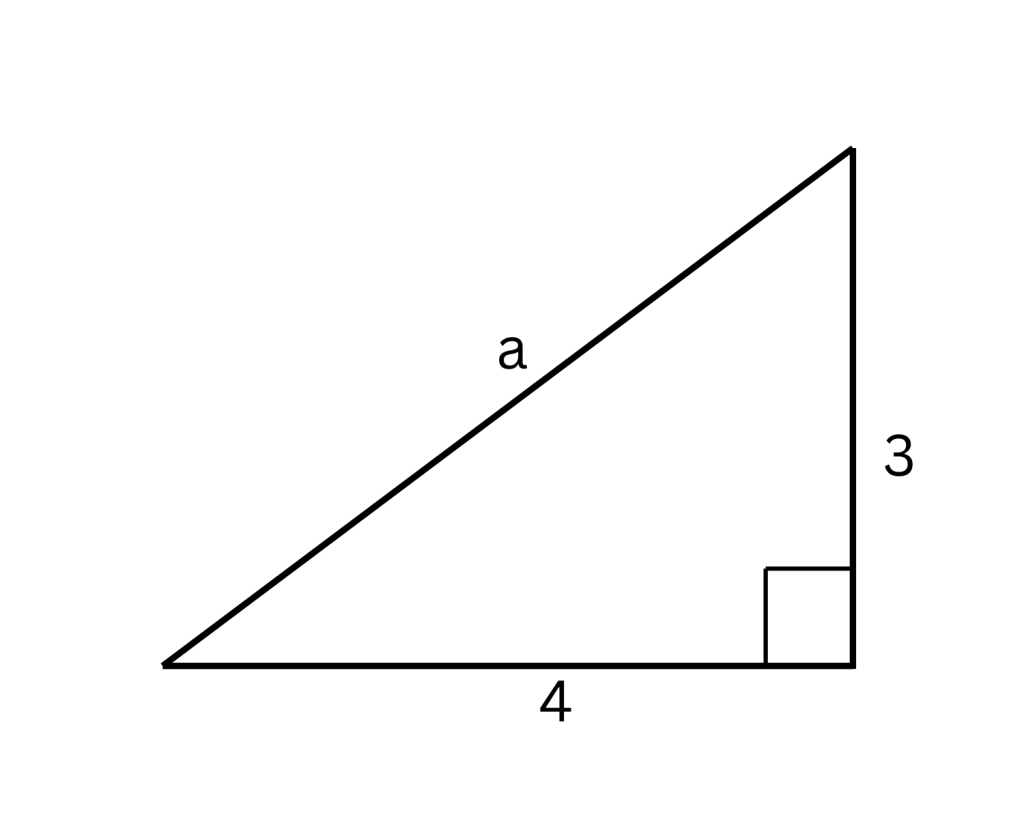
(Using the Pythagorean Theorem:
a² = 3² + 4²
a² = 9 + 16
So, a= √25 = 5)
2. An equilateral triangle has three sides of the same length, and each of its angles has the same measure.
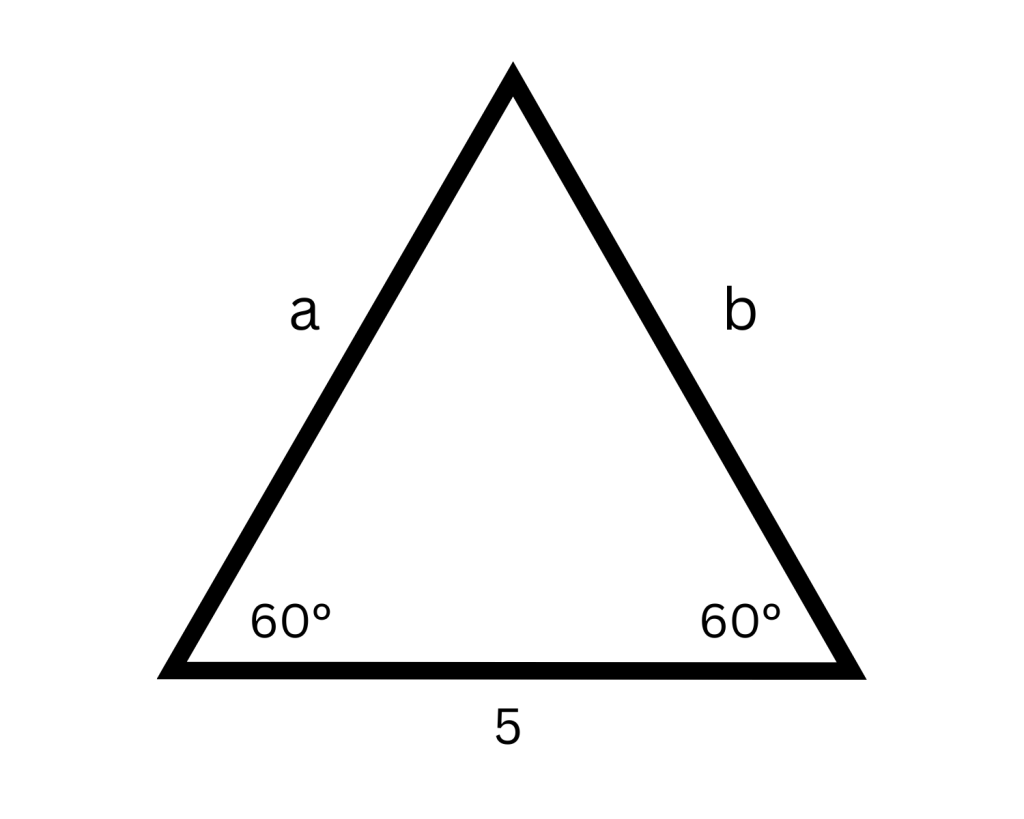
(Since the unmarked angle measures 60°, and all angles in the triangle are equal, it follows that all three sides of the triangle must also be the same length.)
3. In an isosceles triangle, if two sides are the same length, then the angles across from them are also the same. Likewise, if two angles are equal, the sides opposite those angles must be equal as well.
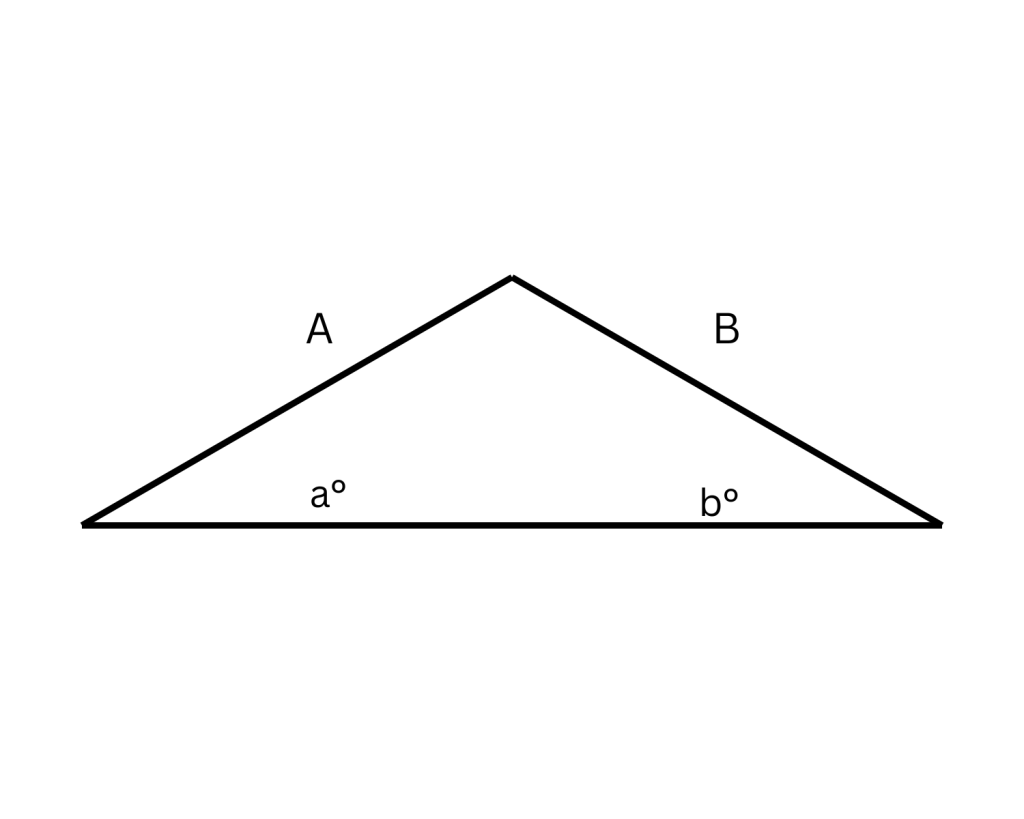
4. In every triangle, the side across from the biggest angle is the longest, and the side across from the smallest angle is the shortest.
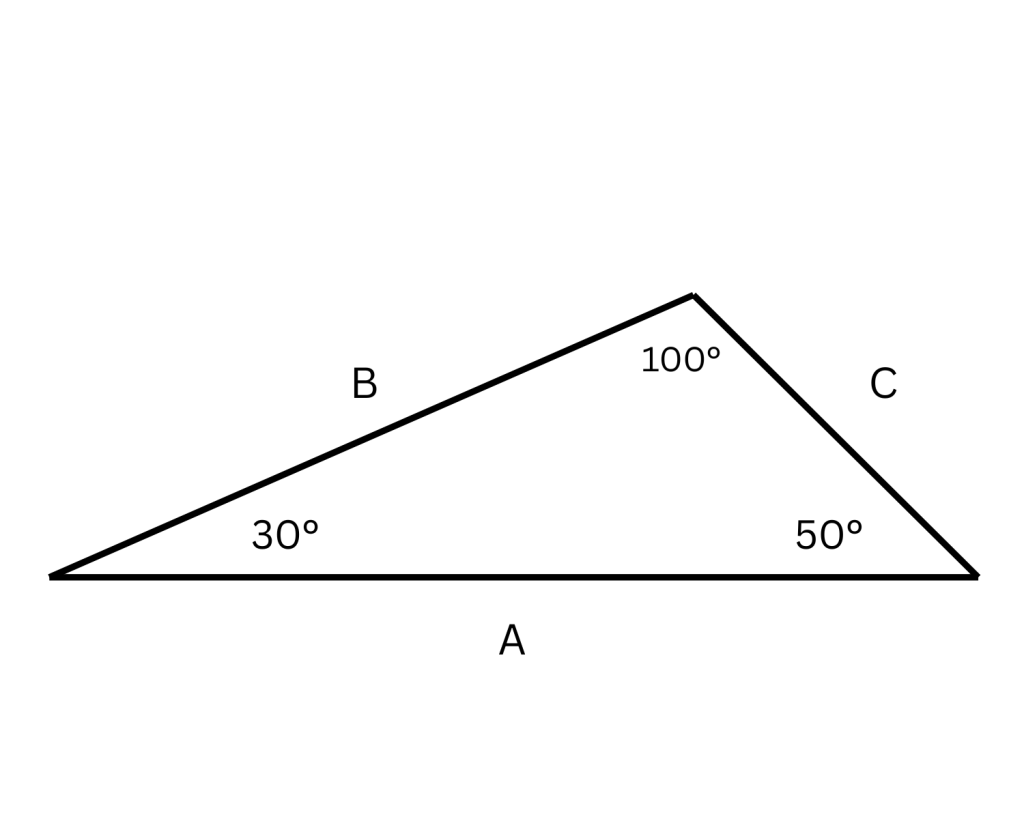
5. Two polygons are considered similar when their matching angles are equal and the lengths of their corresponding sides have the same proportional relationship.

Area and Perimeter
Rectangles
- The area of a rectangle is found by multiplying its length and width:
Area = length × width = l×wl \times wl×w - The perimeter of a rectangle is the total distance around it, calculated as:
Perimeter = 2 × (length + width) = 2l+2w2l + 2w2l+2w
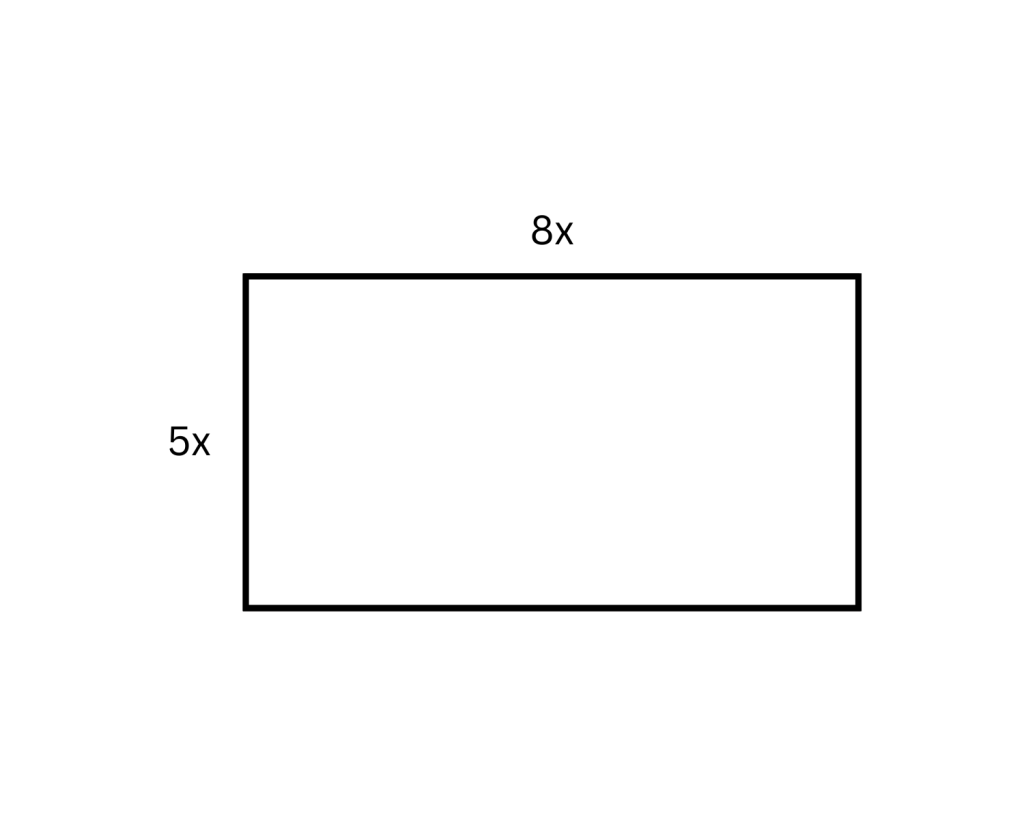
Perimeter = 2(5x +8x) = 2(13x) = 26x
Circles
- To find the area of a circle, use the formula: Area = π × r², where r represents the radius.
- The circumference (distance around the circle) is calculated as: Circumference = 2πr or πd, where d is the diameter.
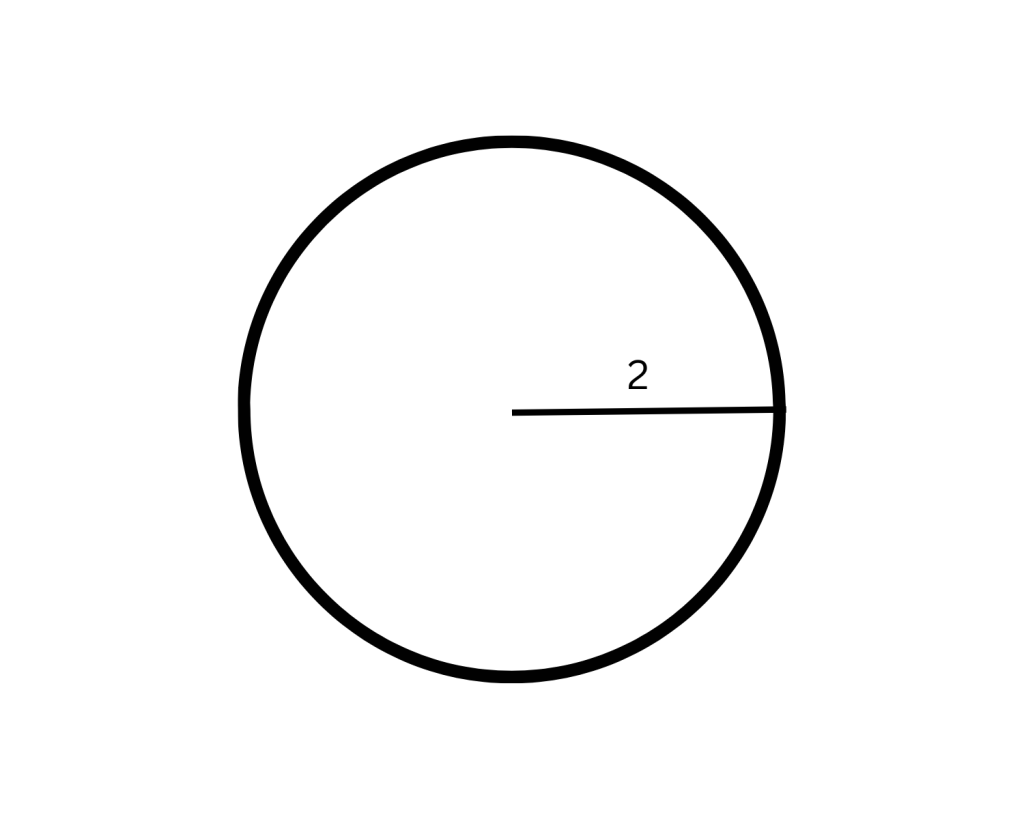
Circumference = 2π x 2 = 4π
Triangles
- The area of a triangle is calculated as: ½ × base × height
- The perimeter is found by adding the lengths of all three sides
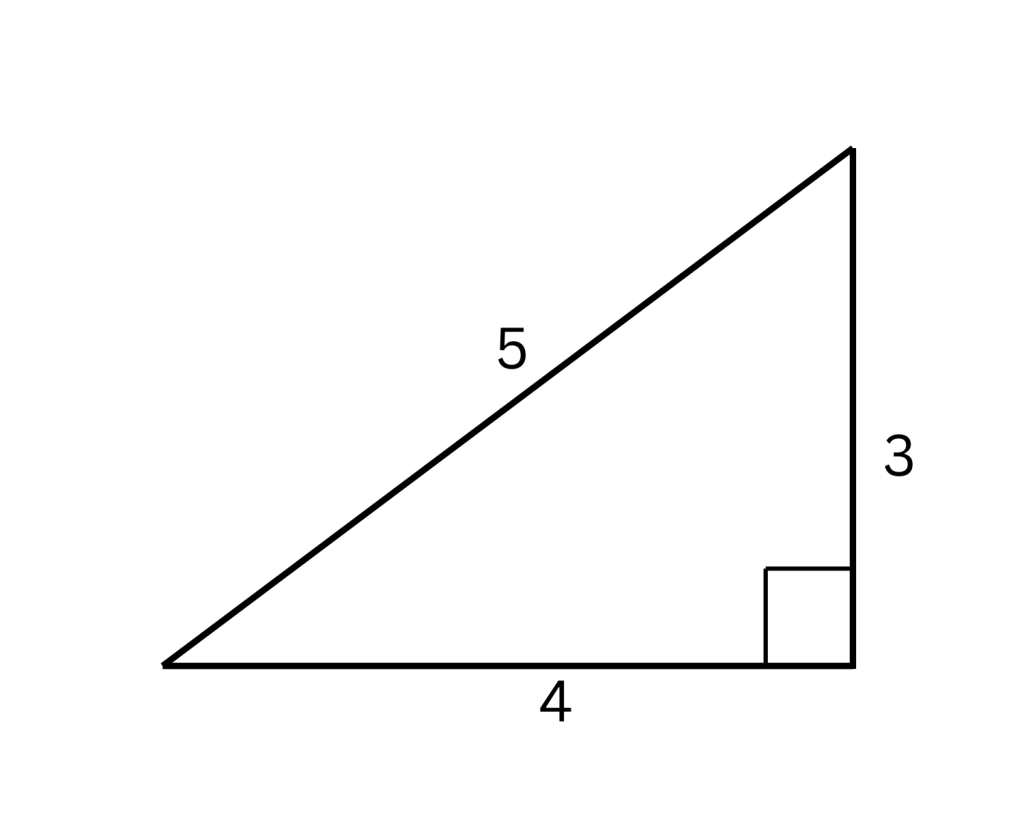
Perimeter = 5 + 4 + 3 = 12
Volume
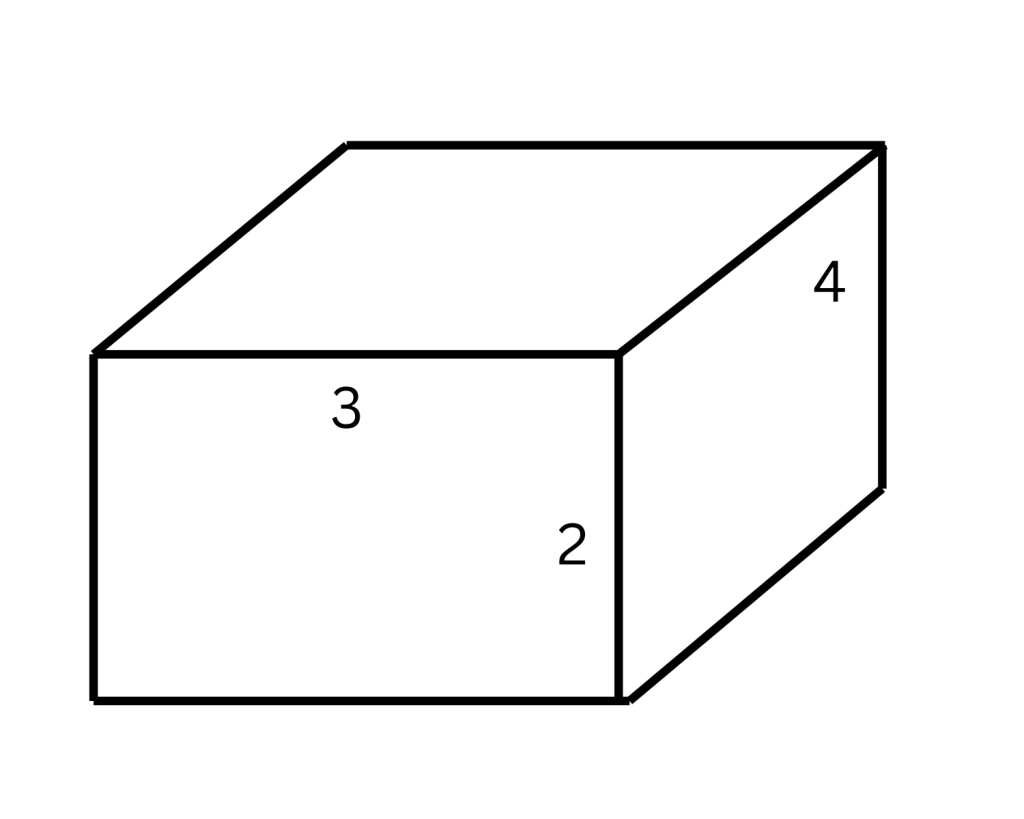
Volume of a Rectangular Solid or Cube
To calculate volume, multiply the length, width, and height:
Volume = length × width × height = l×w×hl \times w \times hl×w×h
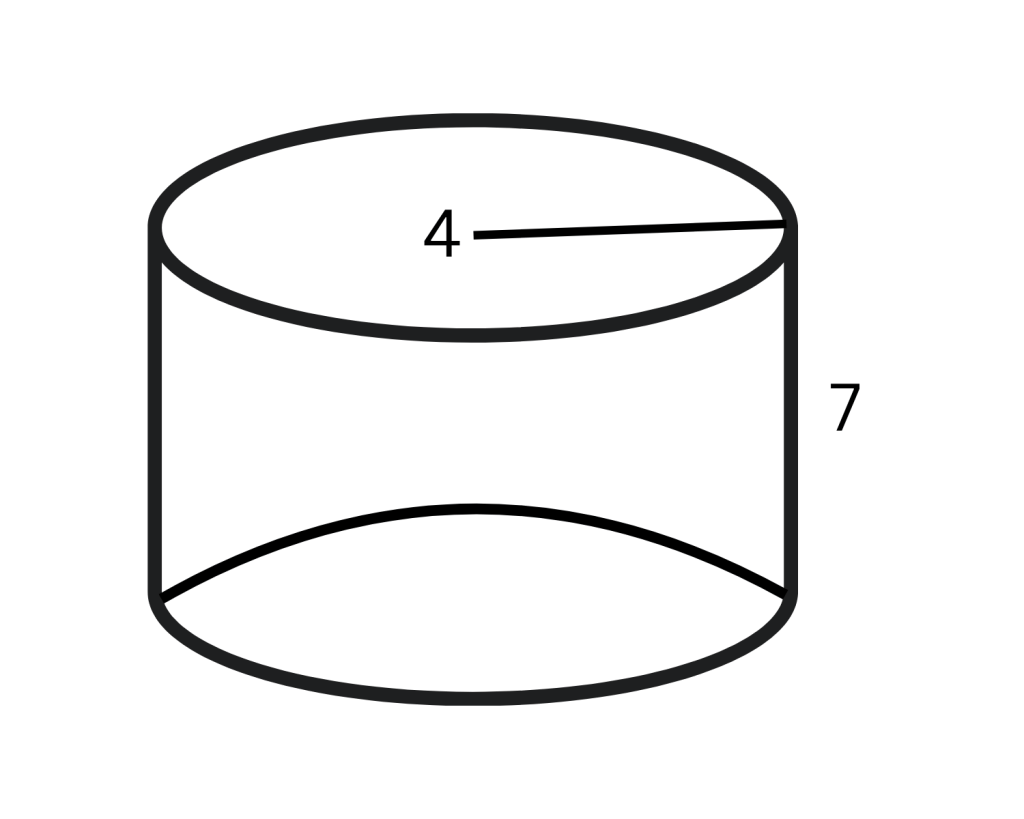
Volume of a Cylinder
The volume of a cylinder is given by the formula:
Volume = π × r² × h,
where r is the radius of the base and h is the height of the cylinder.
Coordinate Geometry
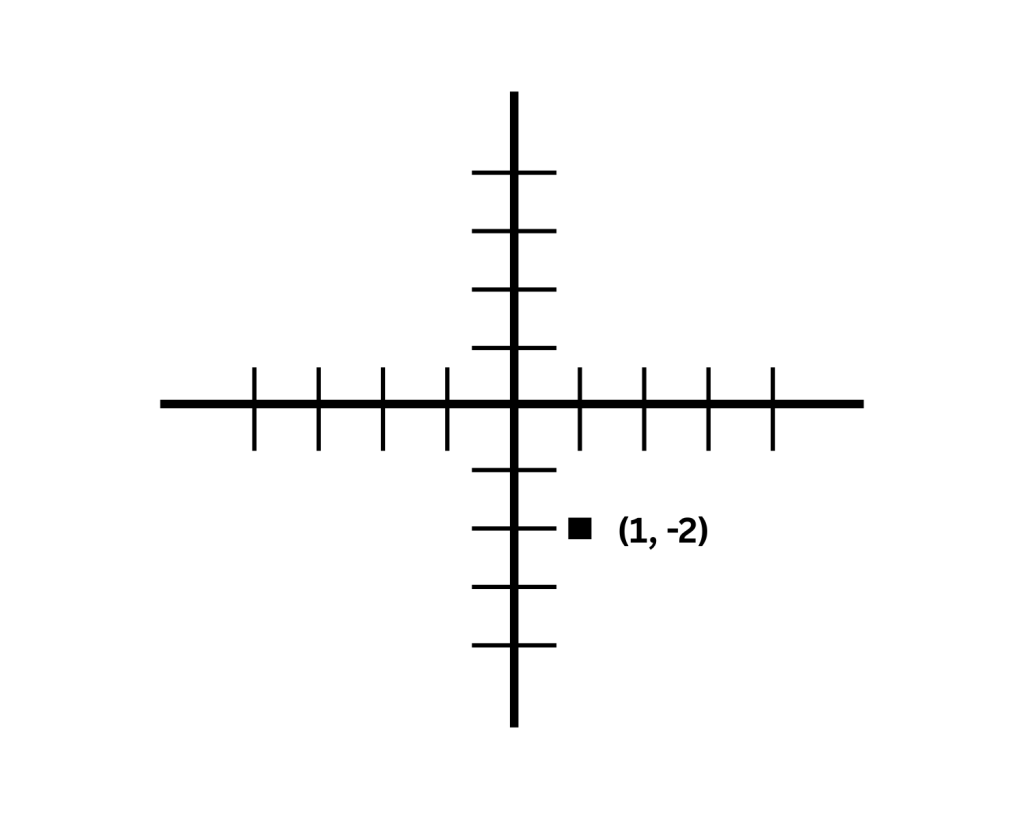
In problems involving the coordinate plane, x-values are positive to the right of the y-axis and negative to the left. Similarly, y-values are positive above the x-axis and negative below it. Ordered pairs are written as (x,y)(x, y)(x,y), where the x-coordinate comes first and the y-coordinate follows.
For example, in the point (1,−2)(1, -2)(1,−2), the value 1 is the x-coordinate, and -2 is the y-coordinate.
The slope of a line represents how steep it is and can be calculated as:
Slope = rise ÷ run, or change in vertical position ÷ change in horizontal position.
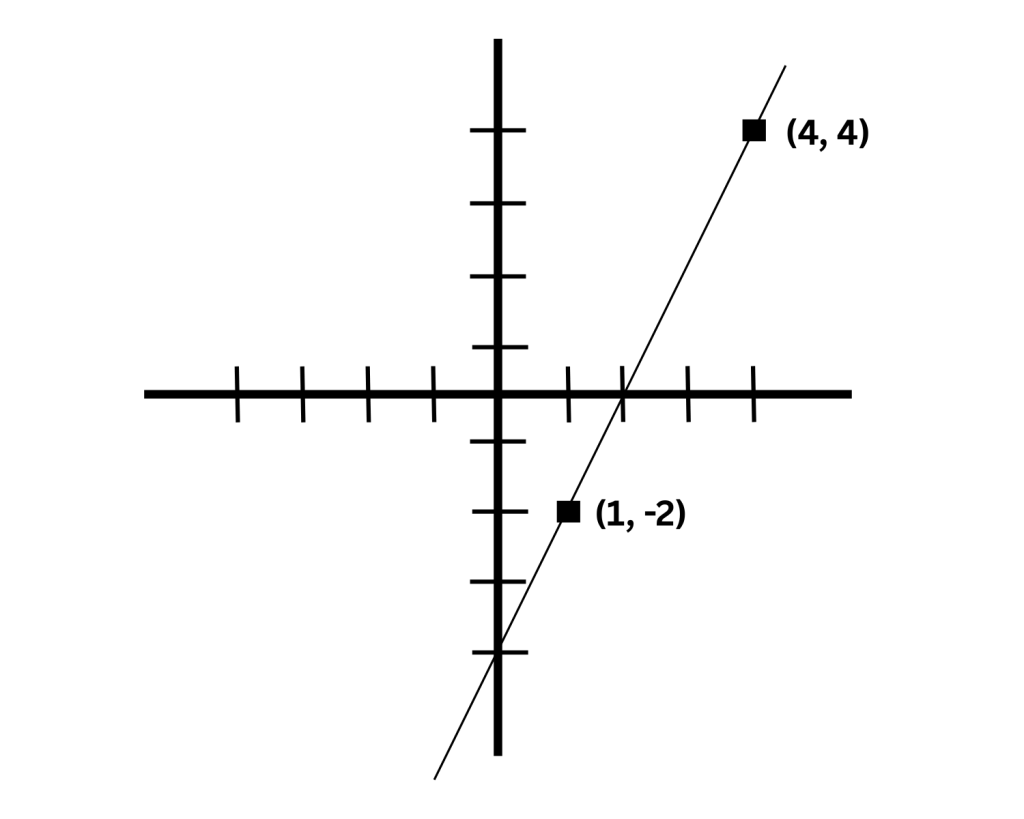
This line passes through the points (1,−2)(1, -2)(1,−2) and (4,4)(4, 4)(4,4). To find the slope, use the formula:
Slope = (change in y) ÷ (change in x) = (4 – (-2)) ÷ (4 – 1) = 6 ÷ 3 = 2
A line has a positive slope when it rises as you move from left to right.
A line has a negative slope when it falls as you move from left to right.